1. Introduction
I am Ginés Salar, Aerospace Engineer by University Carlos III (Madrid, Spain). As this years‘ GSoC edition comes to an end, allow me an opportunity to give a comprehensive explanation of my contributions to aerospaceresearch.net. From my university’s department of aerospace research, there is an interest to develop and test preliminary trajectory optimizers. This has led, in recent years, to the development of MOLTO (Multi-Objective Low-Thrust Optimizer). Such a tool would provide a two-step optimization process for one in three scenarios conceived: IT (Inteplanetary Transfers), OR (Orbit Raising) and 3BP (Three Body Problem). In this post I will not go into the details of these engines but I strongly advice the interested reader to access [GSoC 19′ |UC3M ] MOLTO – Mission Designer.
My efforts try to improve upon the MOLTO-3BP, specifically the first step. The classical approach to this problem searches for a set of ballistic trajectories patched by instantaneous impulses. It is assumed that by reducing the fuel consumption of these impulses, the initial guess improves. After that, the engine moves to the second step and introduces the actual control optimization to adapt the orbit to a truly low-thrust mission. There is little knowledge about whether this procedure delivers the best result or merely a local minimum. Providing an answer to this question is what motivated the work done.
2. Work Breakdown
Parallel works by other students have attempted to provide a database with sampled non-keplerian periodic orbits. Initially, these efforts were aimed to replicate real missions, or to try to improve them using their objectives as a guide. The purpose of this database would be to propagate invariant manifolds from the orbits in order to find ballistic transfers that involve libration point orbits. Finally, the aforementioned patching process is carried out by selecting a suitable Poincaré section and analyzing the trajectories‘ intersections with this surface.
Under this environment, my main objectives were:
- Generalize the capabilities of these functions.
- Structure the code into a single body.
- Translate the existing code to Python.
- Emulate libration point orbits transfers.
- Provide a new metric for the trajectories‘ suitability with a shape-based approach.
The first point, was to isolate all constants from the rest of the code and allow an easy access and control of the studied system. Furthermore, the most interesting libration points, due to the small Jacobi constant required to access their neighbourhood, are the collinear points L1 and L2. We decided that the program should extensively cover both points and the motions around them. This way, the basic building blocks used previously to compute Halo and Lyapunov orbits were extended to be applied to L1 and L2, and tested for the Sun + Earth & Moon system and the Earth + Moon system.
From that, it is important to remember that the purpose of these orbits is to propagate the disturbed trajectories that emanate from them. This promotes the idea of generating a common access point that joins orbit creation and manifold propagation, as well as, post-processing. On that line, I homogenized the input/output requirements of both orbit families and standardized the procedure to any future orbit family. The idea still holds for any non-periodic trajectory that in turn becomes relevant to propagate manifolds from. These steps were crutial to figure out as they are particularly relevant for an eventual integration of this code as part of MOLTO-3BP.
Another relevant point is that the original code requires a Matlab’s licence. This reduces drastically the code’s accessibility from any external sources. This could be easily avoided by converting the code into an open-source language with similar inner workings. The obvious candidate was using Python as it is also a high-level language with similar flexibility to Matlab’s. This change also introduces the possibility of using any of the many freely available modules, such as numpy, scipy, spiceypy and matplotlib. This way of proceeding not only reduces programming time, but also execution times. Additionally, the program can implement features not currently present in Matlab, like the explicit Runge-Kutta method of order 8 included in scipy’s suite. This allows for more precise computations for the most sensitive problems.
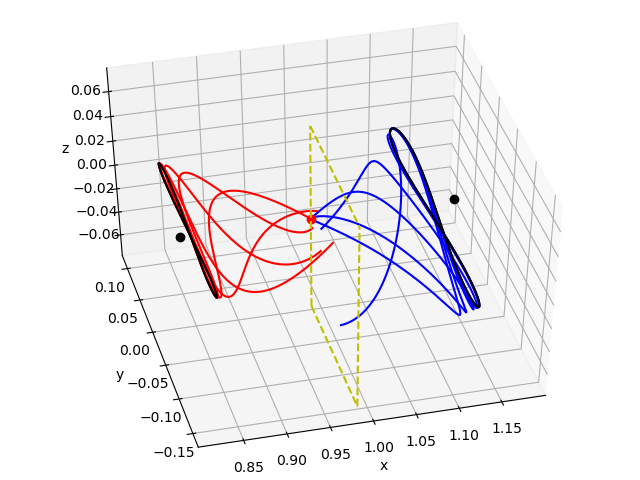
Following the reshaping of the code, several testing ideas and possible future developments arose. One of the most relevant was the concept of emulating complex sequential orbit transfers, both homoclinic and heteroclinic. The code was provided with the necessary tools to discriminate which manifolds where required by the process plus the ability to iterate both the orbit generation and the manifold propagation processes.
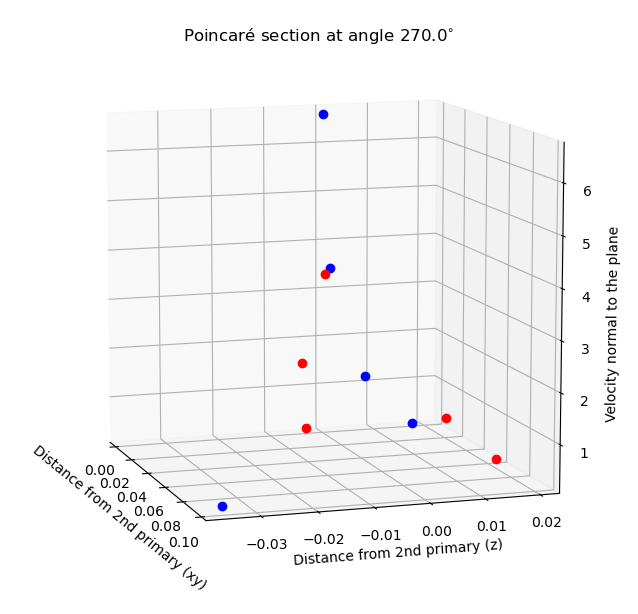
Finally, the end objective was to reach a better understanding of the suitability conditions in order to provide better decision metrics for future optimizers handling this problem. This section is still under development. The initial idea still remains: reduce the ballistic trajectories to their complex frequencies, compare them, and deduce a figure of merit, such as the delta-v required for jumping among them. Preliminary frequency analysis have been started on top of the tools developed, specially for the 2D simpler case. There are already some promising results but much testing is still required to be able to ensure good performance.
3. Acknowledgments
In order to conclude, I would like to thank Manuel Sanjurjo for his constant and agile support during this enterprise. Without his vision this process would not have been nearly as smooth. Also, I thank David Morante, responsible for the creation of MOLTO, for assisting along the way. On a similar note, I take this opportunity to mention Andreas Hornig, as a fine and efficient manager of the community. Everything has been perfectly clear right from the start. Last but not least, I thank Google for running this program and give this sort of opportunities to students like me, it has been a great experience!
4. Useful Links
- Stored code: Pull request
- Github profile: https://github.com/Ibnmardanis24
- Organization email: gines.salar@aerospaceresearch.net