Hello everyone !
My name is Mario Robert D’Ambrosio and I got selected for GSoC 21 with the University of Barcelona to work on the MOLTO-3BP and MOLTO-IT tracks.
During these weeks I had the pleasure to work with multiple mentors, Brandon Escamilla (brandon.escamilla@outlook.com) and Ginés Salar (100345764@alumnos.uc3m.es)
Our goals commitments were multiple: first and foremost to have an integrated working and refactored repository for the MOLTO-3BP (Refactor Github Link)
And to be able to yield a dynamic, yet simple frontend to consume for the University Carlos III (located in Madrid) students and whoever interested in understanding the dynamic amongst translunar orbits and trajectories.
This is why I worked closely with Brandon and Gines, both in charge respectively of mantaining the service accessible on the university’s server (Brandon) for the MOLTO-IT-API operations and the MOLTO-3BP (Gines).
Secondily, we decided also to focus on revamping the UI of the displayed results and moslty to encapsulate all the brilliant work done by Gines for his thesis into OOP modern factory pattern classes.
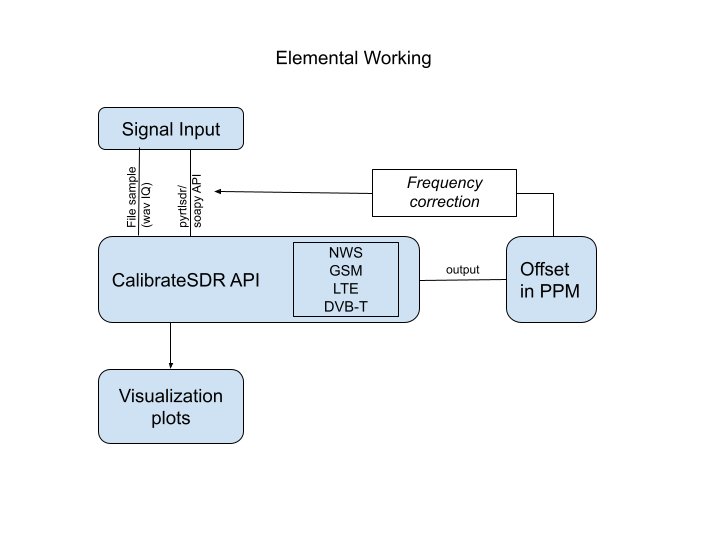
I chose a microservice approach, as a busy python programmer, I decided to go towards this route as microservices communications is easier to manage and mostly, it is the most prominent way to micro-architect projects in the 2021 dev era.
Work Roadmap
- 1. Cleaning up the MOLTO-3BP Repository
First and foremost a cleanup of old files and unused files was done.
I cleaned nearly 30 files and removed many unused pieces of code
- 2. Reformatting the MOLTO3BP Code
Next the code was architectured in small microservices that would allow for the orbits to be computed without incurring in extreme computational weight and or adding sophistication and Massive Controller strategy (https://github.com/uc3m-aerospace/MOLTO-3BP/pull/7/commits/a468244a0ac688391f5a2879f4e22f7759cb6ac0)
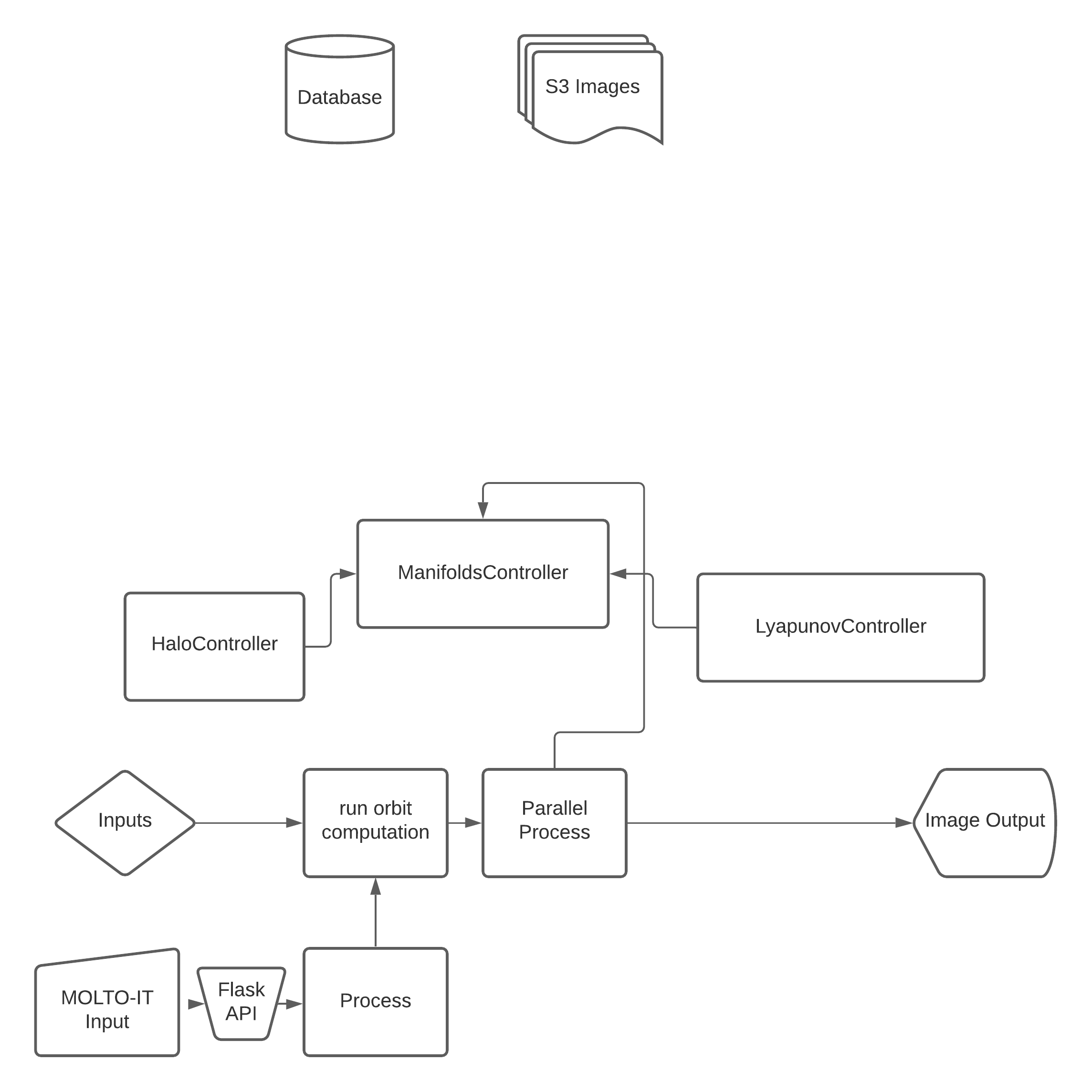
- 3. Adding new running options
The running options were added as a runner in the python file and as static file
Also, clearly, a README was put to explain all the different layers of inputs.
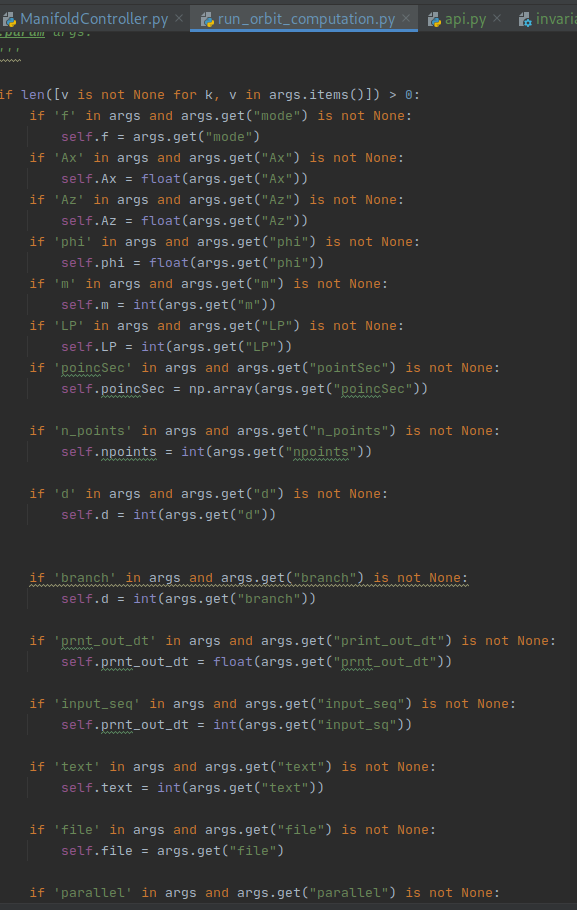
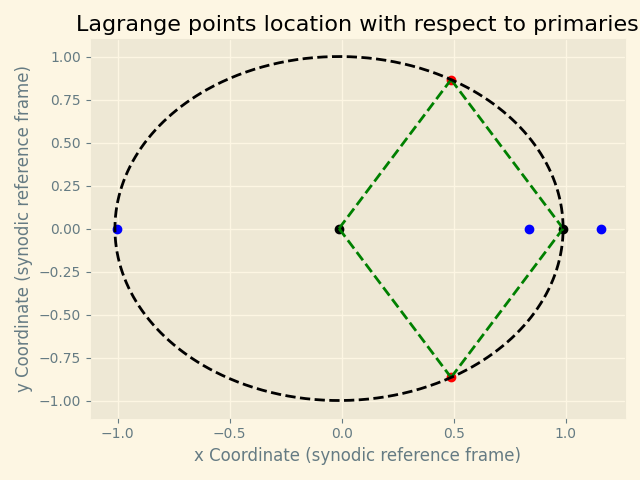
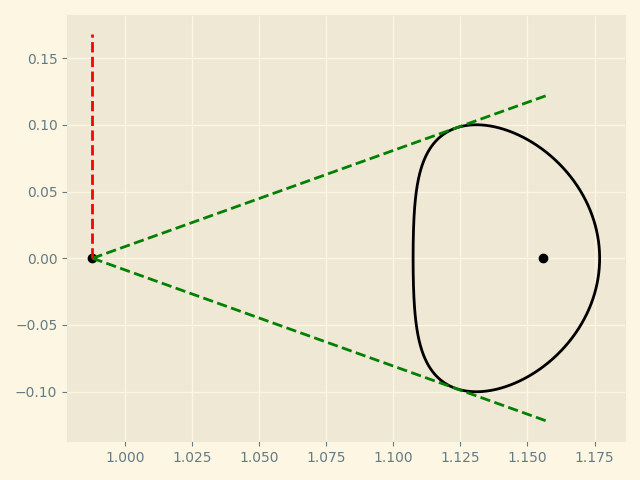
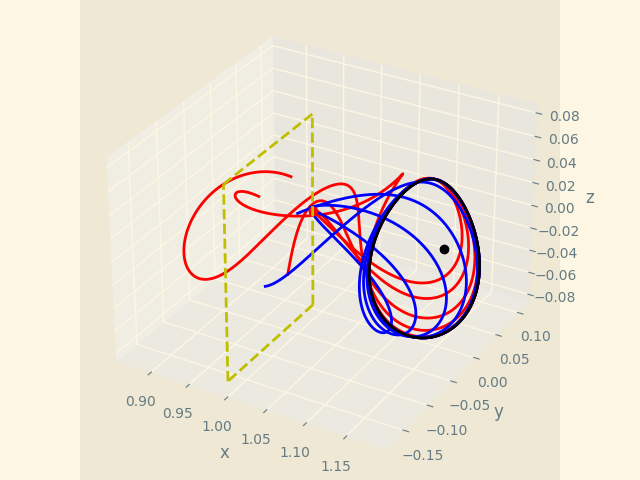
- 4. Changing Image Layout
I have changed the layout in various sessions and offered custom plot graphic display
- 5. Adding multiprocessing
Multiprocessing support for server and scalable core split was also added
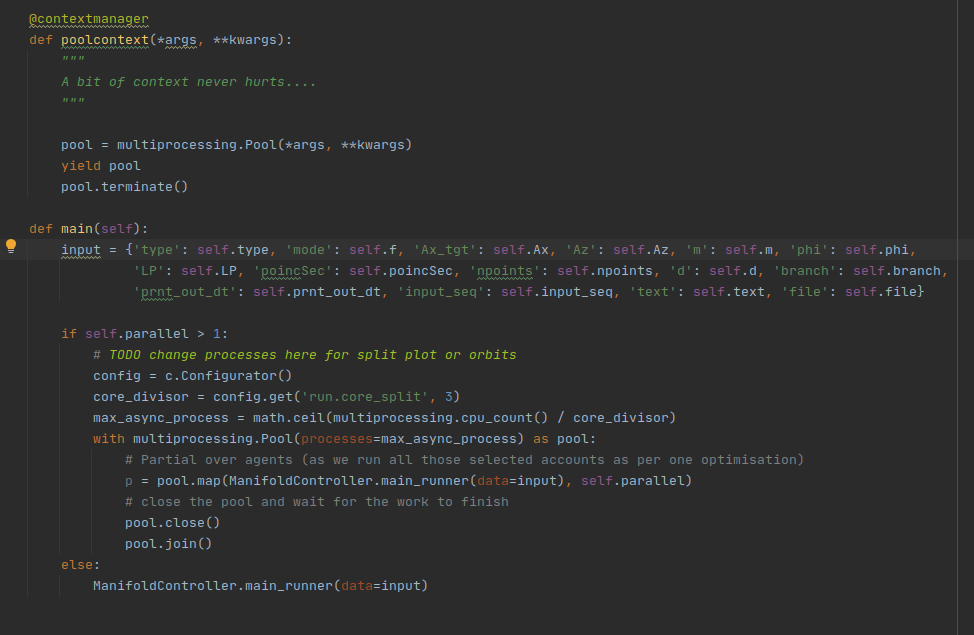
- 6. Adding Flask Support
Finally, to consume the results as QUEUE and display the image with an interrogation system by JOB ID a Flask support was mandatory and added.
This would allow to consume the API and have the results ready asynchronously by calling with JOB ID
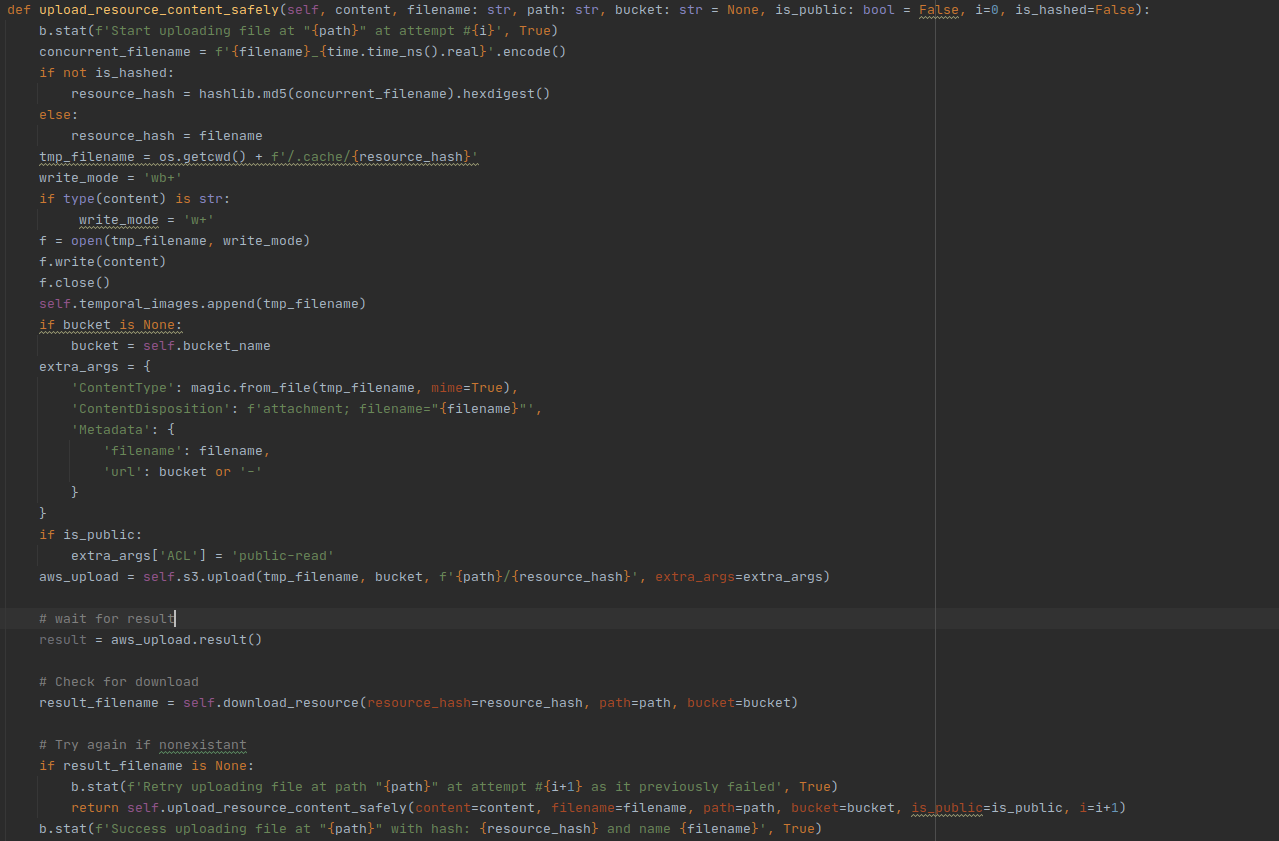
- 7. Adding S3 resource saving support
I have added S3 Bucket support not to bloat the server and consume credits I’ve won on my AWS account in order to display the image results of plots continuously for students.
Snippets of code:
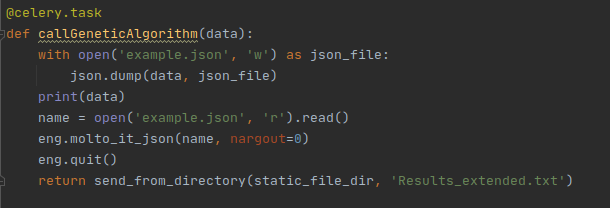
- 8. Finally wrapping it into MOLTO-IT-API
Finally all the code was wrapped into MOLTO-IT, which needed some substantial repolishing and many features/packages upgraded in order for it to work.
Many code snippets were deprecated and, were thus, updated.
https://github.com/uc3m-aerospace/MOLTO-IT-API/pull/2/commits/8f4535e30023899f7a366507cacad533e721a025
Future work
Migration of API to FastAPI
As for the MOLTO-IT we would definitely like to expand and change some things.
Especially we would need to migrate the API to FastAPI to provide more flexibility and maintanance on the long run for the functions and portability.
Also genetic algorithm population and generations could be bettered calibrated to run in a case-specific solution scenario instead of just a plain global one.
This is going to be done by September – October 21 and could be finished in a new GSoC edition.
MAKING THE MOLTO-IT STATIC
It would be nice to dockerize and make the Molto IT static and folder/system agnostic, instead of having many code blocks hardcode as such
Lissajous Orbit
We also plan to work on the Lissajous orbit, which requires most of the computation, as it represents both a blend of the Lyapunov and Halo computations combined.
This is planned to be done by November – December 21.
Conclusion
I have learned so much from such experience, I would be capable of writing an essay for the enormous tasks learnt throughout such experience.
First, communication was essential for the deployment and delivery of the project.
Second, I learned about pacing myself and downplaying my expectations as to aiming high but delivering less is worse than aiming a bit lower and overdelivering.
I tried to aim at a not so fantasmagoric intention but have a GSoC plan and post GSoC plan.
My intentions were to being able to mantain and bring to life a repository where anyone could possibly contribute and deploy new open source code.
I think such intentions were achieved as we have now cleaned up a lot of code and created documentations (MOLTO-3BP -> https://github.com/uc3m-aerospace/MOLTO-3BP/pull/7/commits/0f3ca55a027e8541cc96d79956fbd1f98468116e, MOLTO -IT, MOLTO-IT -> https://github.com/uc3m-aerospace/MOLTO-IT-API/pull/2/commits/8f4535e30023899f7a366507cacad533e721a025)
As a Computer Engineer student, I have always shared a great passion for computer engineering problems and as an aerospace passionate, I enjoy amusing myself with astrophotography and amateur telescope obsevations.
To close the GSoC 21 edition, I went and made my first ascent to the Corno Grande of Italy (https://en.wikipedia.org/wiki/Corno_Grande), where I went to the astronomical observatory and made a night climb to the peak (2912m) to challenge myself and close the GSoC edition with a bit of salt (and pepper! as this is not an easy hike/climb, experts only advised!).
I am grateful to have joined this GSoC edition and to be able to contribute in the future!




![[GSoC2021] CalibrateSDR GSM Support](https://aerospaceresearch.net/wp-content/uploads/2021/07/CalibrateSDR-1.png)