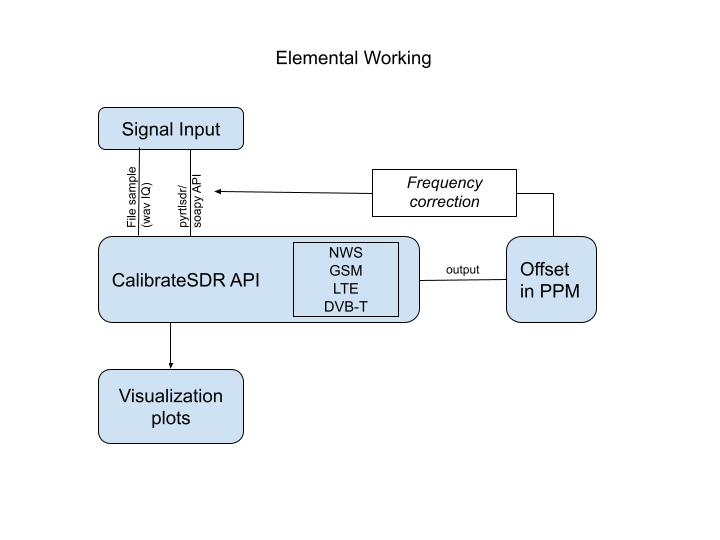
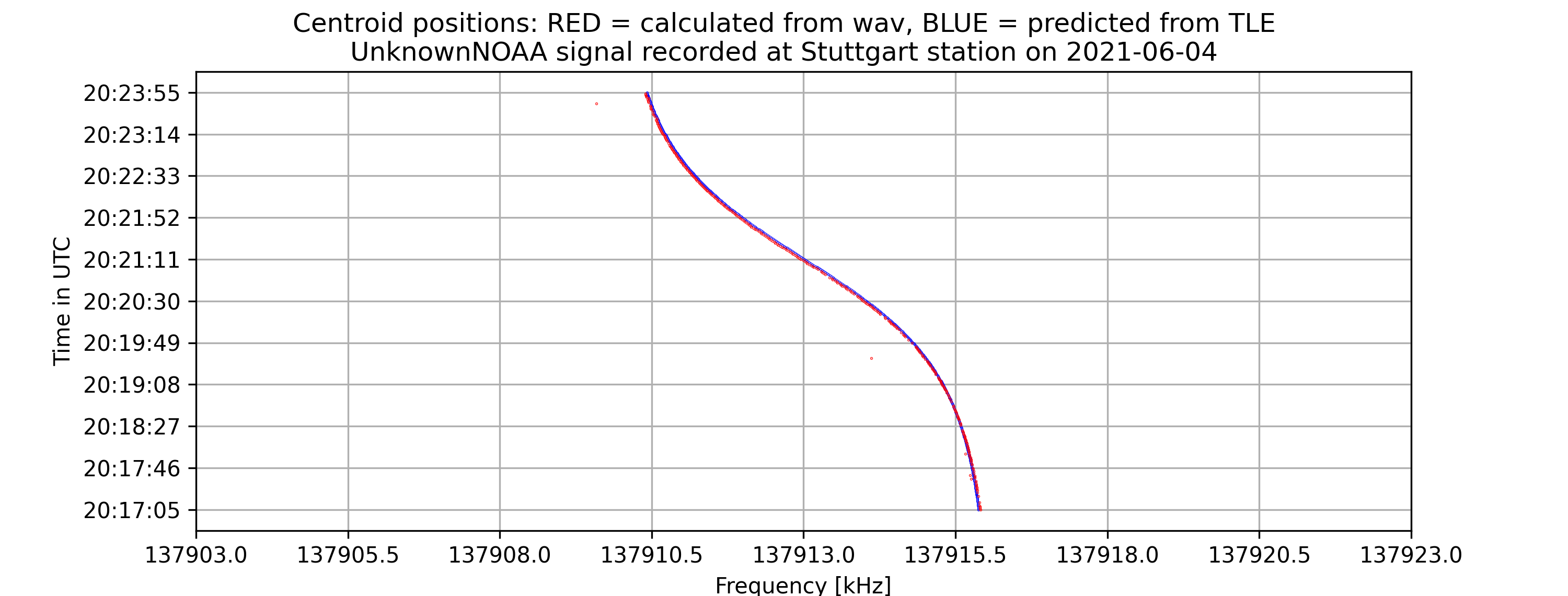
Hi everyone. I am writing this blog to share my work progress with everyone out there.
I have been working on extending the limitations in the Calibrate-SDR tool by adding support of DVB-T and DVB-T2 (terrestrial) signals. Because these signals are broadly used in Europe, Africa, Australia, and Asia region. So can be used here to provide calibration to more SDR users.
Visit here – http://www.dtvstatus.net/map/map.html
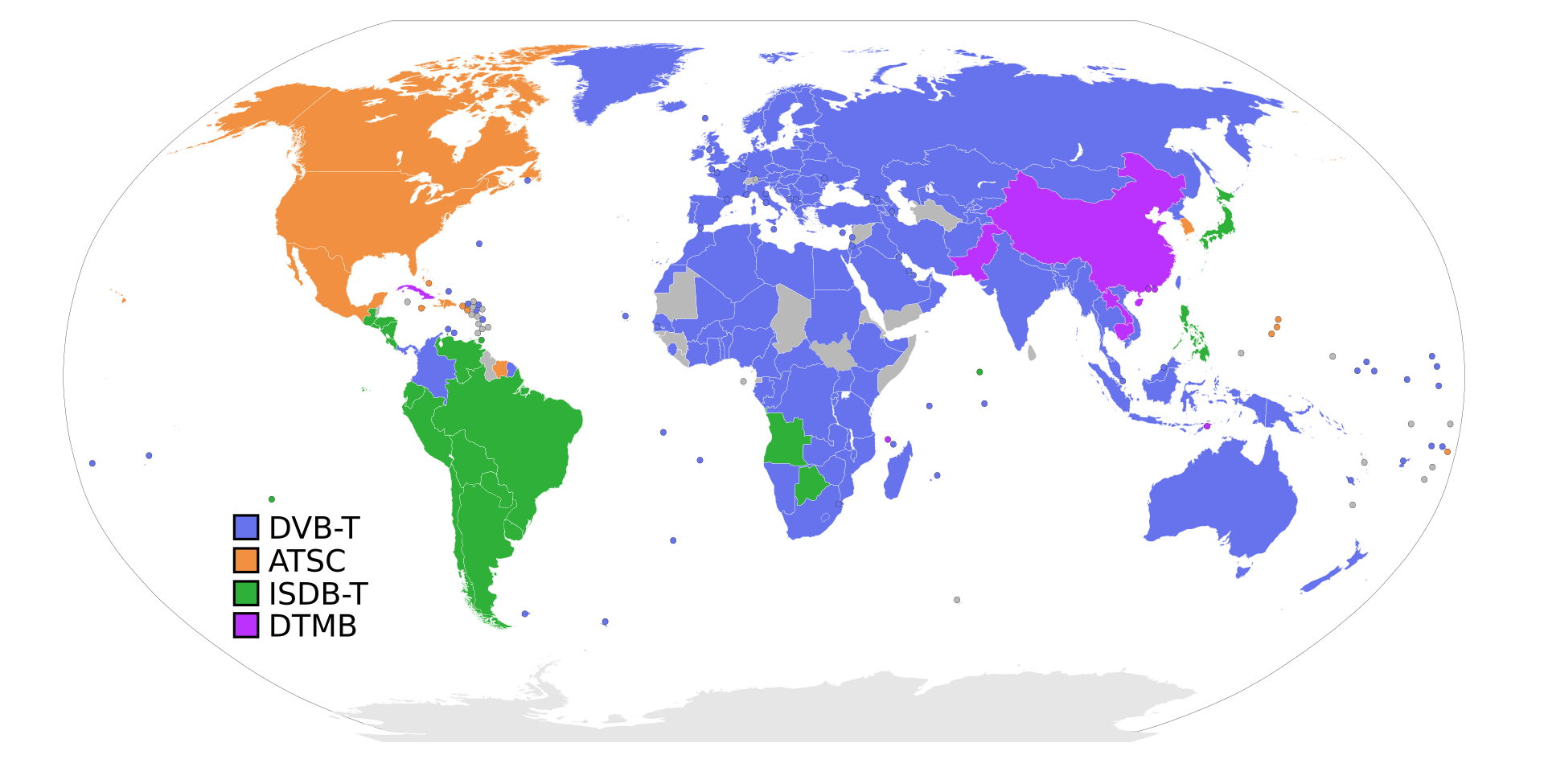
So the question arises What exactly I’m I doing?

As many of you would have worked on some sort of SDRs, might have faced errors due to the Frequency Offset of the Device(due to Crystal oscillators heating).
So here we have a tool named Calibrate-SDR to save you from correcting frequency offset repetitively. Calibrate -SDR is based on the idea of synchronization of devices by a constant frequency part present in the signal. This tool currently uses DAB+ signals to calculate the PPM shifting in frequency. I am enhancing it by using the DVB-T signal for this purpose and try to help more people out there.
Further reading about initial Calibrate-SDR refer to this blog.
Some words of wisdom about DVB-T signal
DVB-T, short for Digital Video Broadcasting — Terrestrial, is the DVB European-based consortium standard for the broadcast transmission of digital terrestrial television that was first published in 1997[1] and first broadcast in Singapore in February 1998. This system transmits compressed digital audio, digital video, and other data in a MPEG transport stream, using coded orthogonal frequency-division multiplexing (COFDM or OFDM) modulation. It is also the format widely used worldwide (including North America) for Electronic News Gathering for transmission of video and audio from a mobile newsgathering vehicle to a central receive point.
Wikipedia
Thanks to Wikipedia for providing historical details about this signal.
Some Technical Details about signal.
Would suggest reading the technical standard for more detailed idea about it.
https://www.etsi.org/deliver/etsi_en/300700_300799/300744/01.06.02_60/en_300744v010602p.pdf
I would cover only the part that was of value for me. Going through this paper and some research. I found out that DVB-T signals have a constant part called pilot inside the ODFM frame structure of DVB-T.
So in addition to the transmitted data an OFDM frame contains:
– scattered pilot cells;
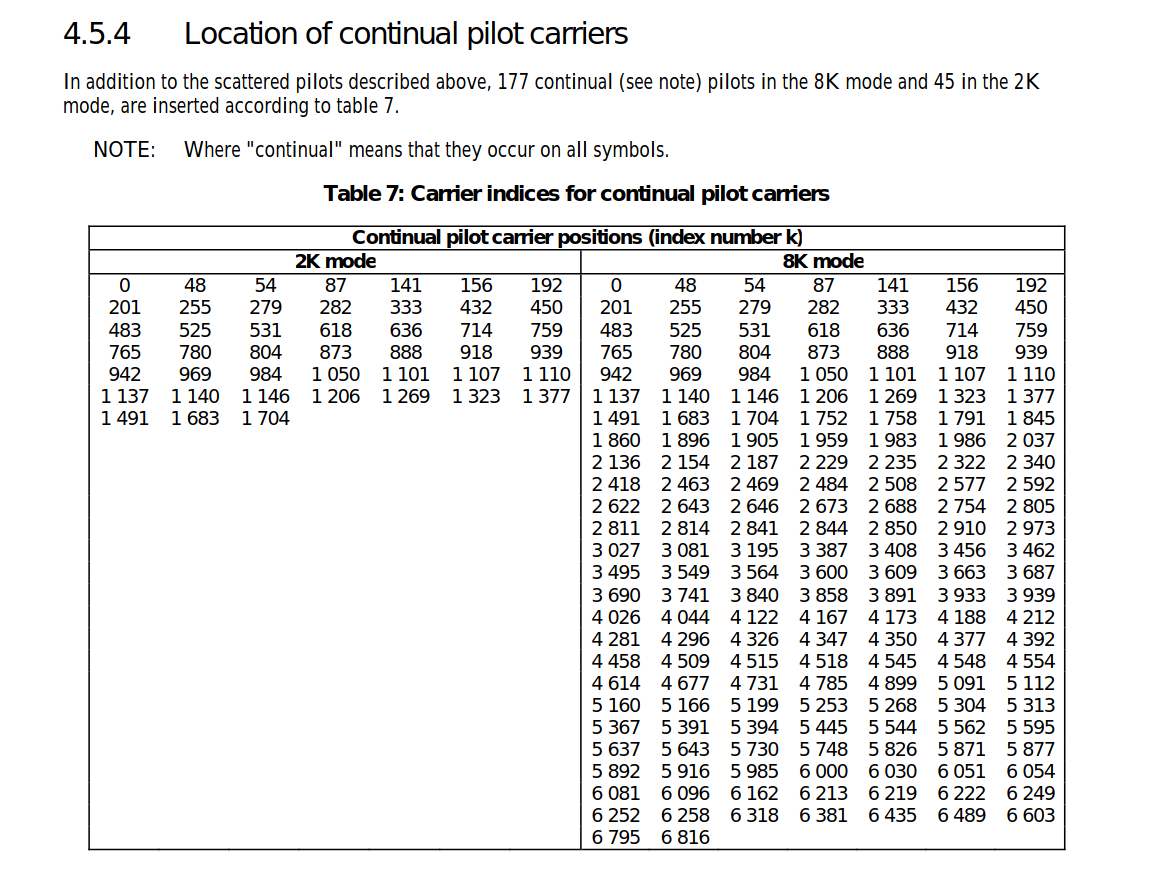
– continual pilot carriers;
– TPS carriers.
The modulation of all data cells is normalized so that E[c × c∗]= 1.
All cells which are continual or scattered pilots are transmitted at “boosted power level” so that for these E[c ×c∗] = 16/9.
The pilots can be used for frame synchronization, frequency synchronization, time synchronization, channel estimation, transmission mode identification and can also be used to follow the phase noise.
The carriers are determined by Kmin = 0 and Kmax = 1 704 in2K mode and 6 816 in 8K mode respectively. The spacing between adjacent carriers is 1/TU while the spacing between carriers Kmin and Kmax are determined by (K-1)/TU.
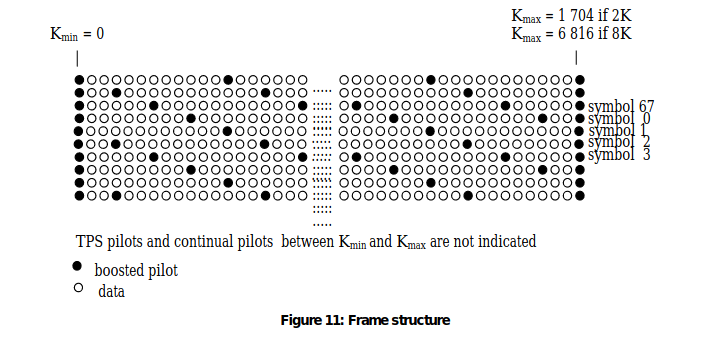
The numerical values for the OFDM parameters for the 8K and2K modes are given in tables for 8 MHz channels, for 6 MHz and 7 MHz channels.
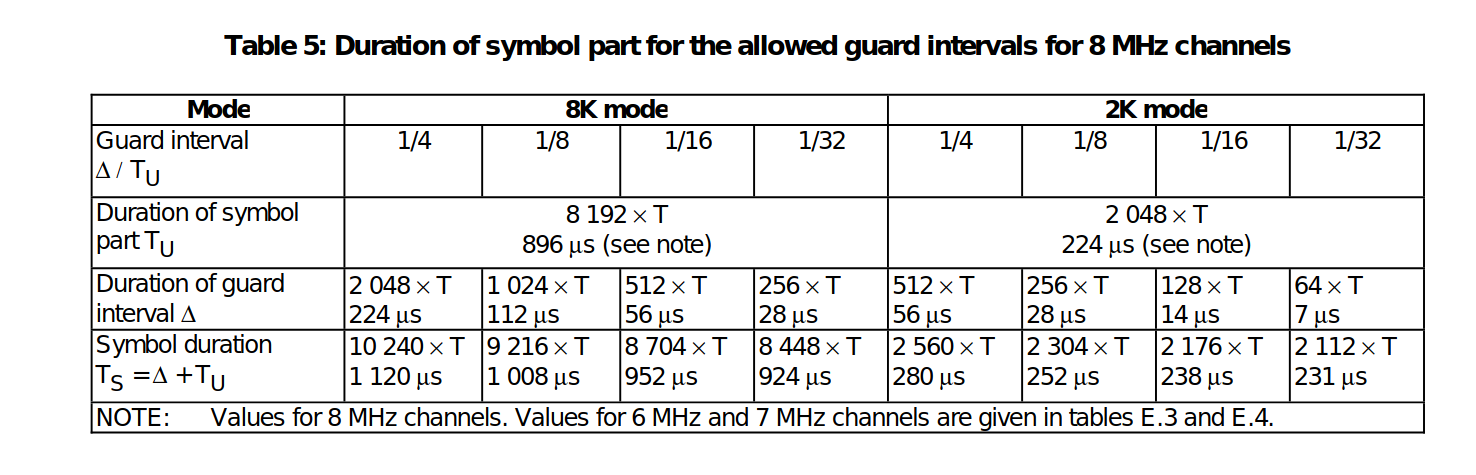
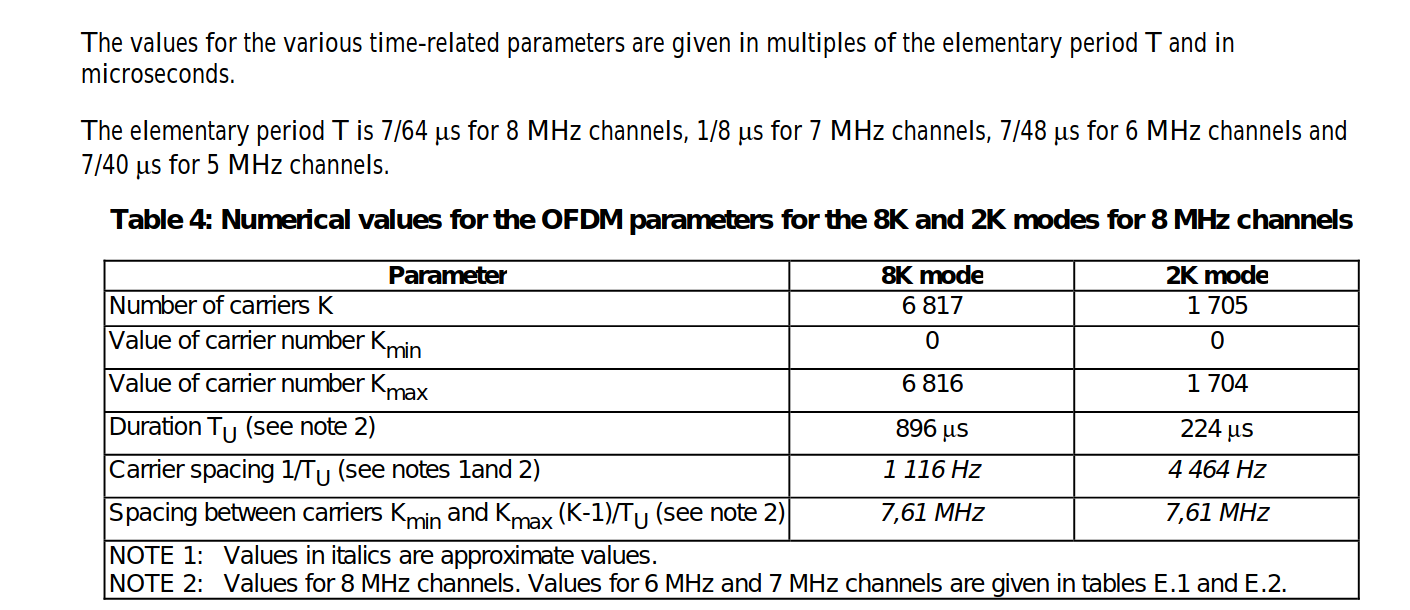
We would collect some continual pilots and average them to get an overall current frequency. We would create an array of all the indexes of the continual pilot and use it.
Then we would subtract them with the known frequency of DVB-T. Hence, we would have the PPM shift. So that’s much of what we are doing for our tool.

It’s more interesting to work on once done with the boring Research work.
Anonymous Developer
Links –
Link to working repository is – https://github.com/AerospaceResearch/CalibrateSDR/tree/dvbt
I am attaching a test file too for a better understanding of this tool. Test file
Some more paper –
https://ca.rstenpresser.de/~cpresser/tmp/dvbt_7_paper.pdf
https://www.ese.wustl.edu/~nehorai/paper/Radar_Harms.pdf
http://ntur.lib.ntu.edu.tw/bitstream/246246/200704191002918/1/01258670.pdf
More Chat on-
https://www.linkedin.com/in/ayush-singh-101/
https://aerospaceresearch.zulipchat.com/#narrow/stream/281823-CalibrateSDR/topic/Signal.3A.20DVB-T

![[GSoC2021] CalibrateSDR GSM Support – first coding period](https://aerospaceresearch.net/wp-content/uploads/2021/06/CalibrateSDR-1.png)