[GSoC2021: findsatbyrf] Summary of the first 5 weeks

By Binh-Minh Tran-Huu on 2021-07-15

1. Introduction

Because of the recent sharp growth of the satellite industry, it is necessary to have free, accessible, open-source software to analyze satellite signals and track them. To achieve that, as one of the most essential steps, those applications must calculate the exact centers of the input satellite signals in the frequency domain. My project is initiated to accommodate this requirement. It aims to provide a program that can reliably detect satellite signals and find their exact frequency centers with high precision, thus providing important signal analysis and satellite tracking statistics.

2. Overview

The project aims to locate the exact centers of given satellite signals with the desired accuracy of 1kHz, based on several different methods of finding the center. At first, the center-of-mass approach will be used to determine the rough location of the center. More algorithms will be applied from that location depending on the type of the signal to find the signal center with higher accuracy. 

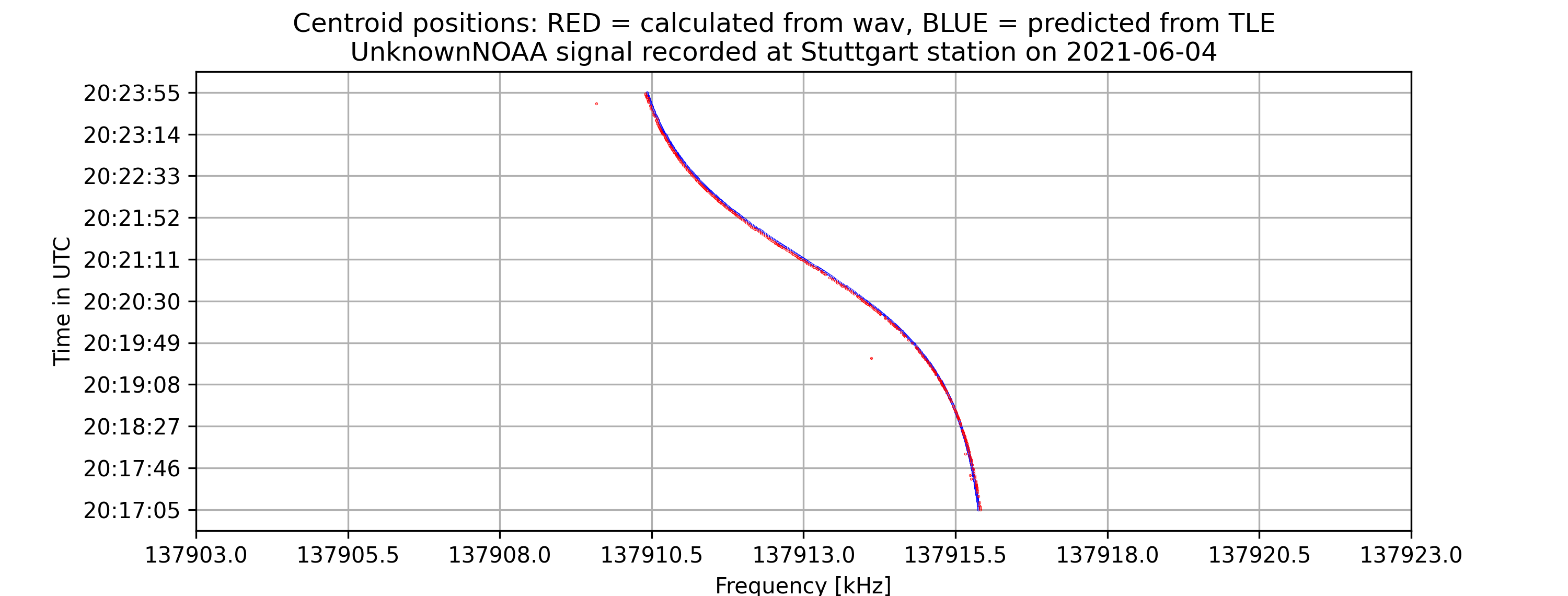
Currently, for many NOAA signals, with the center-of-mass and “signal peak finding” approach (that will be shown below), we can get results with standard errors less than 1 kHz. For example, with the following signal, the standard error is 0.00378 kHz.

3. Theoretical basis

The overall flowchart

1. Fast-Fourier Transform (FFT)

Fourier Transform is a well-known algorithm to transform a signal from the time domain into the frequency domain. It extracts all the frequencies and their contributions to the total actual signal. More information could be found at Discrete Fourier transform. 

Fast-Fourier Transform is Fourier Transform but uses intelligent ways to reduce the time complexity, thus reducing the time it takes to transform the signal.

2. Noise reduction and background signal reset

There is always noise in actual signals, but generally, noise has two important characteristics: normally distributed and its amplitude does not change much by frequency. You can see the signal noise in the following figure:

If we can divide the signal in the frequency domain into many parts such that we are sure that at least one of them contains only noise, we can use that part to determine the strength of the noise.

For example, consider only this signal segment:

By taking its average, we can find where the noise is located relative to the amplitude 0. By subtracting the whole signal to this average, we can ensure the noise all lies around the zero amplitude.

Next, we want to reduce all the noise to zero. To do that, we consider the distribution of noise, which is a normal distribution.

Photo from Characteristics of a Normal Distribution.

From this distribution, we are sure that 99.9% of noise has an amplitude less than three times the noise standard deviation. If we shift the whole signal down by 3 times this standard deviation, 99.9% of the noise will have amplitude less than 0.

From there, we can just remove every part of the signal with an amplitude less than zero. Then we will be able to get a signal without noise with the background having been reset to 0. 

You can clearly see the effect of this algorithm by looking at the signal of PIXL1 satellite above, where all the noise has been shifted to below 0.

3. Center-of-mass centering

This algorithm is simple, the centroid position is calculated as (sum of (amplitude x position)) / (sum of amplitude), similar to how we calculate the center of mass in physics. The result of this algorithm is called the spectral centroid, more information could be found at Spectral centroid.

4. Peak finding.

For signals with clear peaks such as APT(NOAA), finding the exact central peak points of the signal would give us good results. From the rough location of the center by the Center-of-mass method, we can scan for its neighbor to find the maximum peak. This peak will be the center of the signal that we want to find. 

For APT signals, this peak is very narrow, therefore this method is able to give us very high precision.

5. Predicted signal centers from TLE

TLE (Two-line element set) information of a satellite can be used to determine the position and velocity of that satellite in the orbit. By using this data of position and velocity, we can calculate the relativistic Doppler effect caused by the location and movement of the satellite to calculate the signal frequency that we expect to receive on the ground.

6. Error calculation.

Assume TLE gives us the correct result of signal center, we can calculate the standard error of the result by calculating the standard deviation:

Where n is the number of samples, x_i is the difference between our calculated center frequency from .wav and the frequency we get from TLE.

4. Implementation in code:

https://github.com/aerospaceresearch/findsatbyrf/tree/bm_dev

• main.py is where initial parameters are stored. The program is executed when this file is run.
• tracker.py stores the Signal object, which is the python object that stores every information about a signal and the functions to find its center.
• tools.py contains the functions necessary for our calculation and the TLE object used for center prediction.
• signal_io.py stores functions and objects related to the input and output of our signal.

5. Current results: For APT(NOAA):

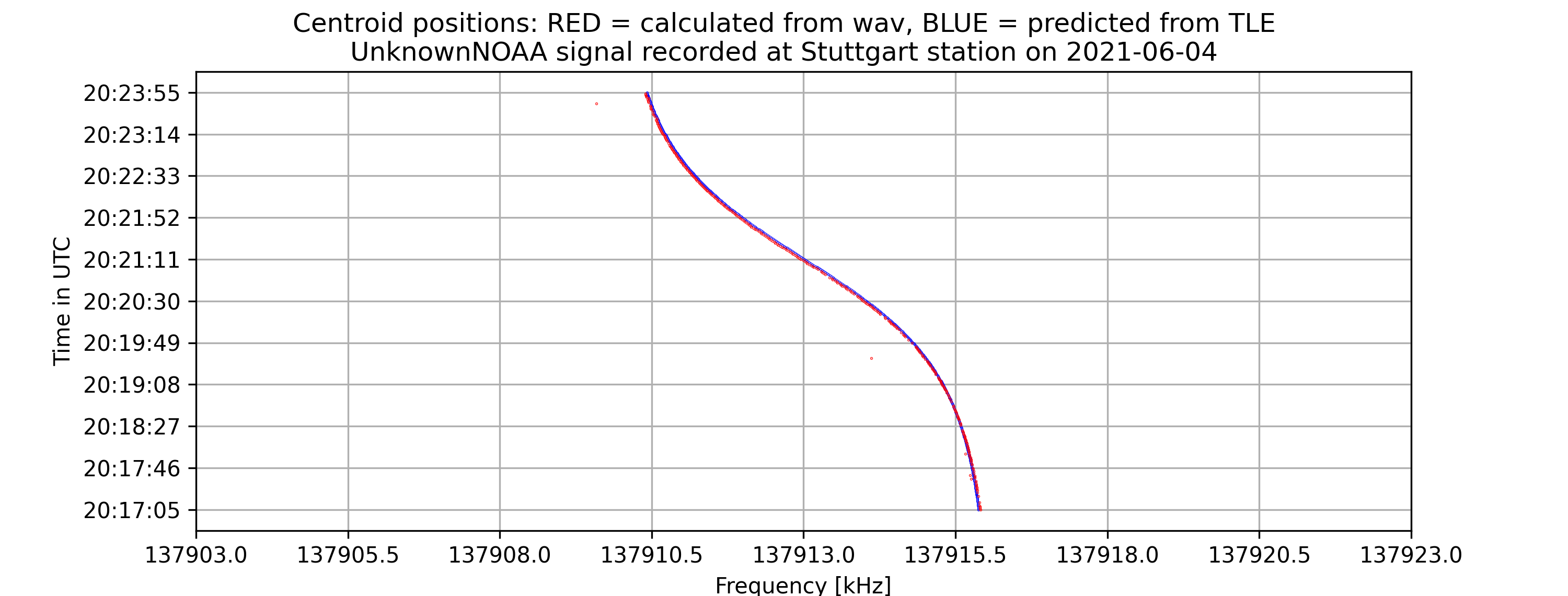
Standard error = 0.00378 kHz

6. Usage instruction:
   1. Create a folder with the name of your choice in the ‘findsat’ folder, for example, ‘data’.
   2. Put the .wav file of your signal in this folder with any name. 
   3. Put a satellite.tle file in the folder containing the TLE of your satellite.
   4. Put a station.txt file in the folder containing the name and location of the ground station where you recorded the signal separated by a “=”, for example (The numbers should be in degrees and meters):
   5. Change the content of main.py as instructed in the code, then run main.py. The result will be put in your ‘data’ folder.

name = Stuttgart

long = 9.2356

lat = 48.777

alt = 200.0

Example of station.txt