Introduction
Mathematics is the field of science which is very vast, and the backbone for all other fields of science. It supports the development of new technologies, and in the development of new technologies. Mathematics plays a very important role in any kind of research and development. I was responsible for developing VisMa, a new project for AerospaceResearch.net under Google Summer of Code – 2017. VisMa, created to create a platform which could solve algebraic equations and perform several other complex functions on it like root finding, integration and differentiation.
The project aims to help people solve complex problems and learn. It can help students in learning concepts. It can be used in research-oriented, double-checking the solution to problems.
Development tools
Python 2.7
PyQt 4.0
Development Process
After the proposal was accepted. The one month community bonding period. I was mostly interacting with Manfred Ehresmann and Andreas Hornig from time to time.
Since this is a new project, a community bonding period has been used. Some GUI mock ups were created by me, so that’s it. The resources for the planning phase and GUI mock ups are available here . This is the first time I use OpenGL, and PyQT 4.0.
It was that VisMa’s code wants to be hosted on AerospaceResearch.net ’s GitHub organization.
Coding period started from 1st June, PyQT 4.0 was used to build the GUI. Some key features of VisMa’s GUI were dynamic buttons. This is the first step in the process. VisMa also has scope for multiple styles of input, for now it’s just normal and LaTeX style. VisMa wants to be able to store a history of older expressions. PyQT had a slight learning curve, but event based programming was pretty straight forward.
Each module was created it such a way that they are independent from all the other modules. This allows us to make changes in one module without effecting any other module. Also allows us to just plug in the modules, and use it with the software with minimal integration steps required.
The final GUI looks something like this:
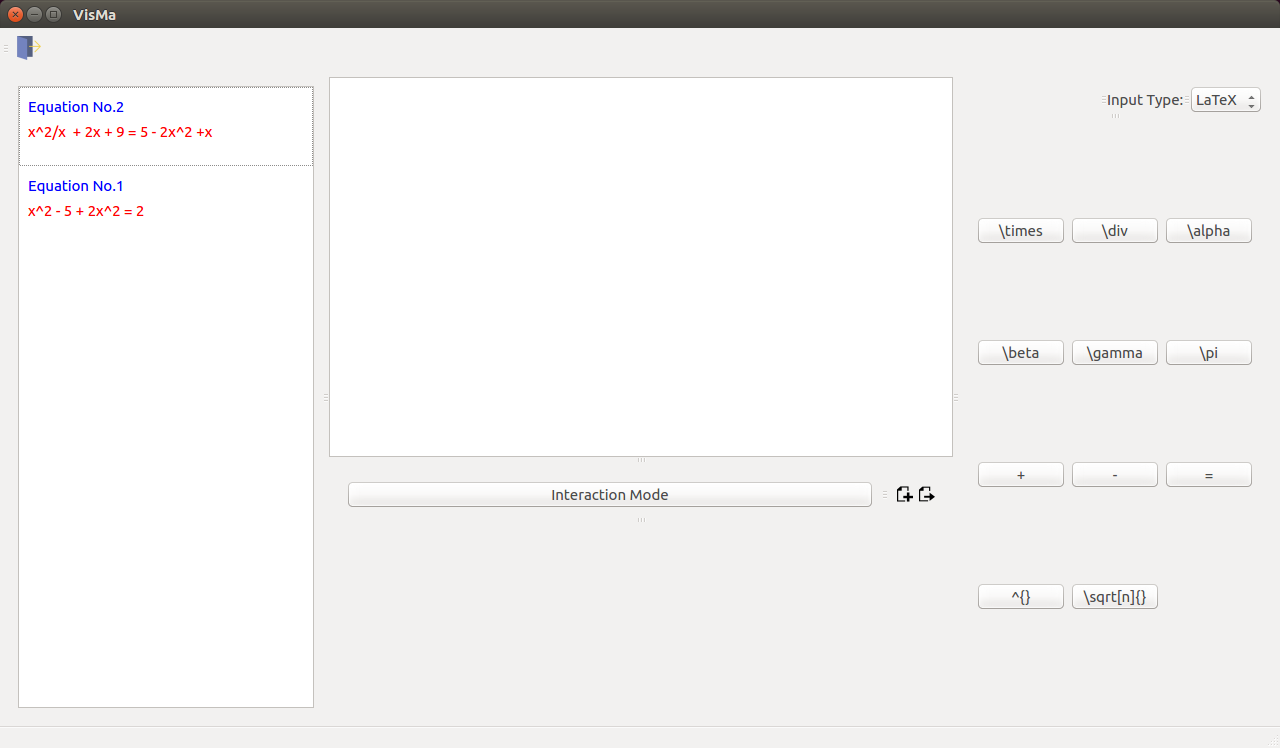
Next task is to convert all supported types of input into a common format, so that it is separate the logic for solving from the types of input. This provides the advantage of a more efficient way of doing things. This is the only way to make a difference between the variable and the variable, but it is also a function of the variable position relative to other tokens. Eg if the input is 2x ^ 2y ^ 4 + 4, it ’s tokenized form would be:
[‚Coefficient‘: ’scope‘: [0, 2], ‚type‘: “ variable ‚,‘ power ‚: [4.0],‘ value ‚: [‚ y ‚]} Type: binary, ‚value‘: ‚+‘, ‚{‚ scope ‚: [2],‘ type ‚:‘ constant ‚,‘ Value ‚: 4.0,‘ power ‚: 1}].
While the tokenized format for: 2x ^ {2} y ^ {4} + 4, will be:
[‚Coefficient‘: 2.0 ’scope‘: [0], ‚type‘: ‚variable‘, ‚power‘: [2.0, 4.0], ‚value‘: [‚x‘, ‚y‘]}, {‚ Scope ‚: [1],‘ type ‚:‘ binary ‚,‘ value ‚:‘ + ‚}: 1}].
This shows how powerful the tokenizer is in distinguishing between different inputs.
This is the most difficult part of GSoC for me, I have to go through over 2k lines of recursive code, check and double check if it works for any type of token, and take care of all the cases. I would like to thank you for your feedback.
Then I proceeded with coding the solving part. A rough data flow diagram of the rest of the architecture of VisMa is as follows:
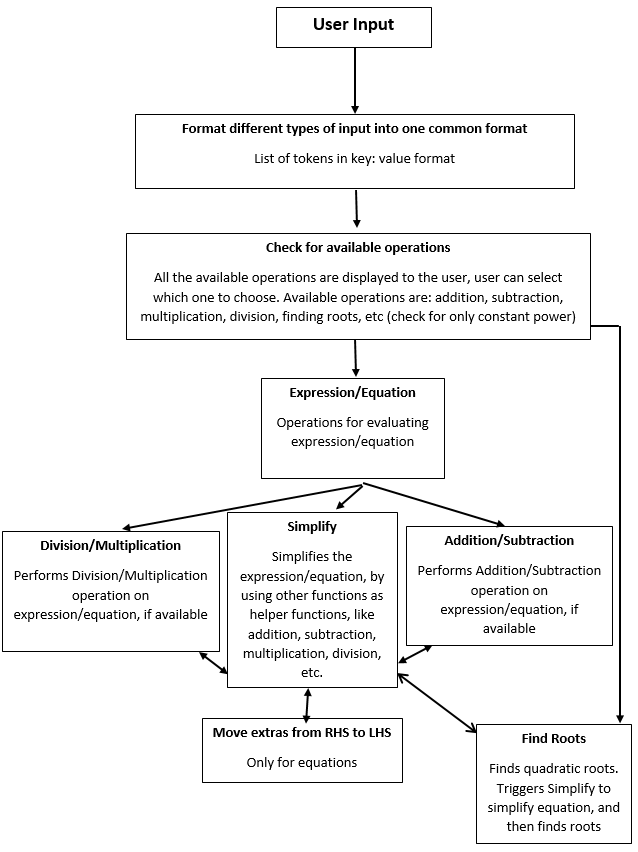
It shows how user input is first converted into a common format, we will call it the tokenized form The user.
The user selects the user’s input, and a step by step.
Next task is to find the available operations. Finding division and multiplication operations were relatively easy, just to find the ‚/‘ or ‚*‘ token. But for addition and subtraction, a little more cumbersome method was selected. I have to create a separate list in which each element (constant and variable) were group together according to their value and power, ie all constants were in one group, while all variables with the same value and the same power were in one group, so x ^ 2 and 3x ^ 2 would end up in one group. This made finding addition and subtraction. Addition and subtraction were not followed by ‚/‘ or ‚*‘.
This function would return all the available functions to the user, and user could either completely simplify the equation or expression, or select either adding, subtracting, multiplying or dividing.
Expression Evaluation
For division and multiplication tasks, the elements were directly divided or multiplied, without any issues. But there is no such thing as a „subset“ of a person’s mind. If there were more than 1 elements in each group and the elements were not followed by ‚/‘ or ‚*‘, then they were added / subtracted. To implement the task of simplification, the above mentioned. After each iteration / task, the list of available operations was updated to see if there is any additional operations available.
Equation Evaluation
For the purposes of the present invention, the present invention is directed to a method and apparatus for evaluating the performance of a vehicle. For LHS and RHS, we have checked for available operations and simplified, then all the elements in LHS would look for elements with similar signatures (constants / variable, if variable, then same value and power) on the RHS, For simplification. In case of equation simplification, the remaining elements on RHS were then moved to LHS. Even for equations, after each iteration / task-performed, the list of available operations.
Another task is done in parallel. The animation module was created by the animation team. During the later course of the development, comments were added to the animation module.
An example of the project:
The example shows how you can use saved equations, and find roots for it. You press on one of the equations in the saved equations list, which you want to solve. In this example, the user selected finding roots, and the whole animation.
Here is another example, which highlights the feature interaction mode:
In this example, it is shown, how the user can input an equation, and select a part of the mouse and its cursor. After that the user can press interaction mode, and all the possible action for it are populated. The user can select one of the, and only the part of the equation / expression selected with the mouse will be processed.
User Guide and Development Manual
An in detail user manual is available on the repository’s GitHub wiki .
The wiki will also work as the development manual, along with the comments in the code.
Acknowledgment
I would like to thank Aerospace Research for giving me opportunity to work with them on a completely Call new project in Google Summer of Code 2017 and I would also like to thank my mentor Manfred Ehresmann for helping me out with this project and helping me through it.
Future Plans
I want to see VisMa getting some enthusiastic reception in the future. I hope to help you. I want to see the graph feature, on which I have been working on the visualization of problem. Improvements in animation, and possible make the animation more interactive. Integration (still in development) and differentiation modules are completed and integrated with it. Create a better abstraction between the solution and GUI module. I want to see VisMa as a unified tool for all mathematics in future.
Useful links
- Source Code : Github
- Documentation : VisMa wiki
- Commits : Commit History
- My Github’s profile : Siddharth Kothiyal