Project overview
In 2017 Google summer of code I was involved in the project by AerospaceResearch.net called „Orbit position data analysis and interpolation“. Mainly, the project focused on methods and techniques that are used to preliminary determine a satellite orbit. More specifically, we initially had positional data sets in the format of (time, x, y, z) and we applied to them some smoothing – filtering techniques (Savintzky – Golay, Triple moving average) and then some methods for preliminary orbit determination (Lambert’s solution, Spline Interpolation). This project was created from scratch, meaning no prior work has been done. It was also applied not only to me, but also to another GSOC student Nilesh Chaturvedi, with whom we had great communication and cooperation leading to some good and interesting working results. The mentor of the project was Andreas Hornig and his insights and guidance provided us lots of help. Before I continue describing some more technical aspects of the project I would like to point out the github repository, which includes all the coding we did as part of the program and the documentation link for the project.
The programming language used for the project was Python 3.4 / 3.5 and libraries that are a core part of the project are Numpy, Matplotlib, Scipy, Pykep and Pytest. The very first coding I did as part of the program was, to get familiar with the data sets we are dealing with and try to perform some basic statistical filtering and create some graphs with matplotlib. Then, I dived deep into smoothing techniques and tried a lot of methods like median filters, FIR filters and Kalman but after many tests, I decided to use the Savintzky – Golay filter which was giving the best results for this kind of data I had. After applying the filter to my data set I quickly moved into creating some code for finding the keplerian elements (keplerian elements = orbit of the satellite) for all these data points I have. I researched a bit about methods for preliminary orbit determination and decided to go for Lambert’s solution and more specifically I decided to use Pykep library which has the method already implemented. So for every 2 points of the 8000 points data (leading to 7999 solutions) set I had, I solved the orbit determination problem and found lots of orbits. Now from all those 7999 different orbits described by 6 keplerian elements, I wanted to find the best approximation and I used Kalman filters to do that exactly. The results at first were not that good but combining my filter with Nilesh’s Triple moving average I managed to get some good approximations. After that, I created code for one more method for preliminary orbit determination called Gibb’s method. That algorithm though was really slow and it was not included in the final version of the program. One future plan I have for the program is to make this algorithm more „light“ so I can include it. Finally, lots of results are printed and graphs about the initial data, filtered data and final orbit are made to ensure the good presentation of the final computations. Into the whole process, lots of sub – functions and calculations needed to take place and they are located in the util directory. Into that directory a user can find algorithms that can transform cartesian to spherical coordinates, two algorithms to transform state vectors to keplerian elements and vice versa, one algorithm with a numerical integration method so that we make the final graph and one for finding the window for the Savintzky – Golay filter.
After finishing the core structure of the program the part of testing arrived, which was divided into two aspects. First was the unit testing with pytest and then massive testing with lots of satellite position data to find what combinations of algorithms function best or what windows and parameters I need to apply to the filters. For the first part, I created 15 general tests that achieved a pretty good coverage.

Now continuing to the most time-consuming part of the project. The massive testing of lots of different data sets occurred, so that we can find whats the best parameters, windows and combinations of our methods. For that data sets, I created a simple script that reads all the data and all the correct keplerian elements from _meta data files and then applies to them the filters and the methods but every time with different parameters and windows. After lots of testing, I came to the conclusion that for Triple moving average the best window to use is 3 and Savintzky – Golay the best polynomial parameter to use is 3 again. For the right Savintzky – Golay window the process is a little more complex and after some more calculations, I designed a simple script that calculates the proper window size based on the length of the data set and the apriori error estimation of the measurements.
The final part of the project was the documentation of it. The use of Sphinx and Read the docs really made that process easier and all the documents that were created by both me and Nilesh are in the github repository. In the documentation, a user can find 3 very useful tutorials on how to use the program, full documentation of all the modules included and an introductory page. Along with the documentation of the project I wrote the code for packaging (setup.py) with setuptools, which was a very interesting task to create and learn.
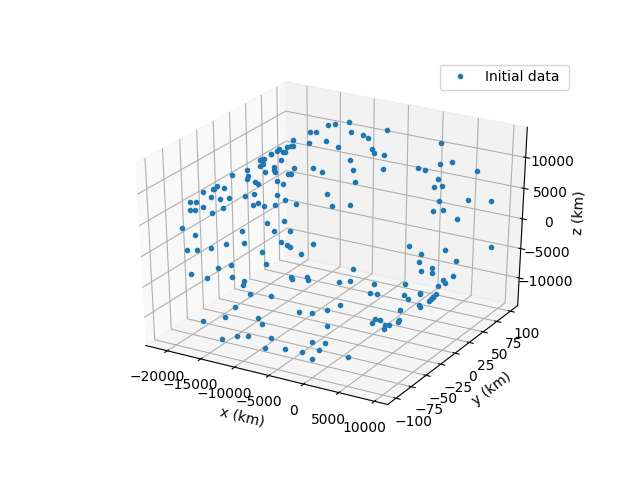
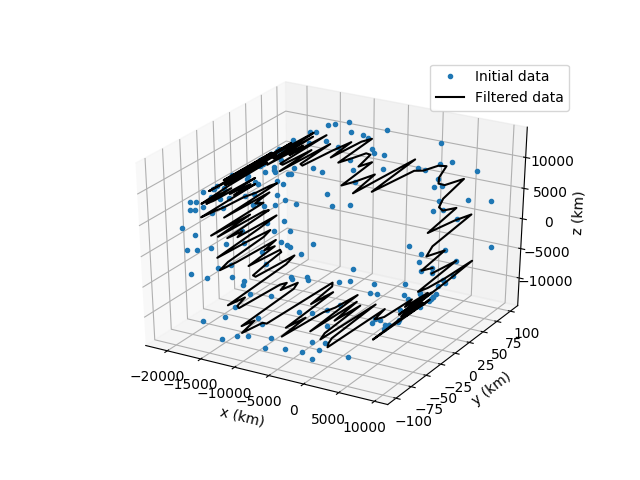
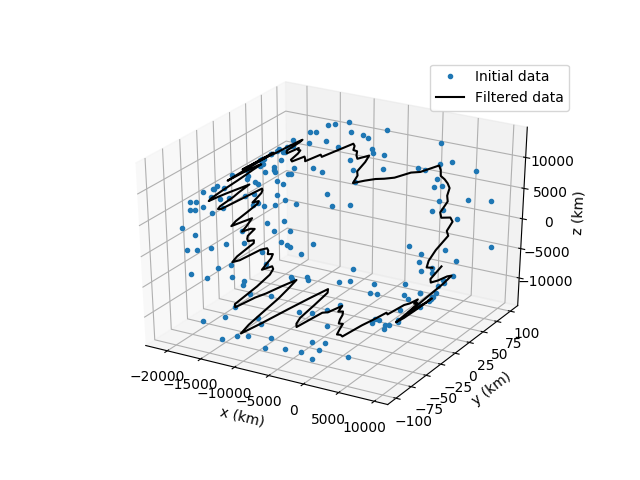
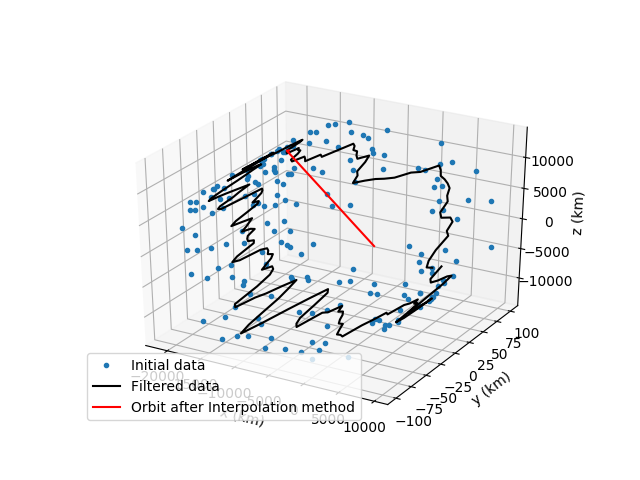
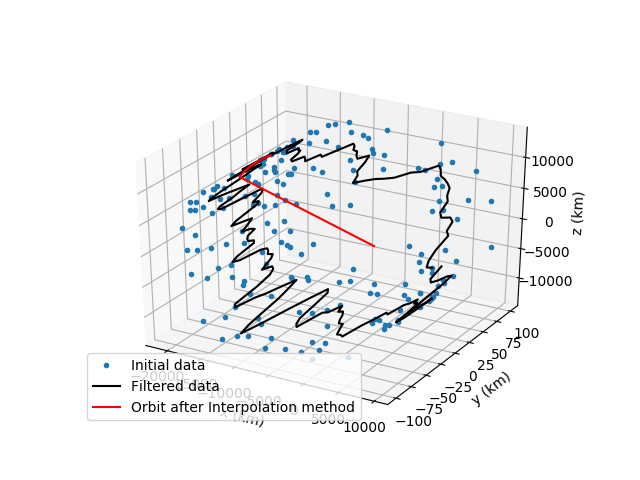
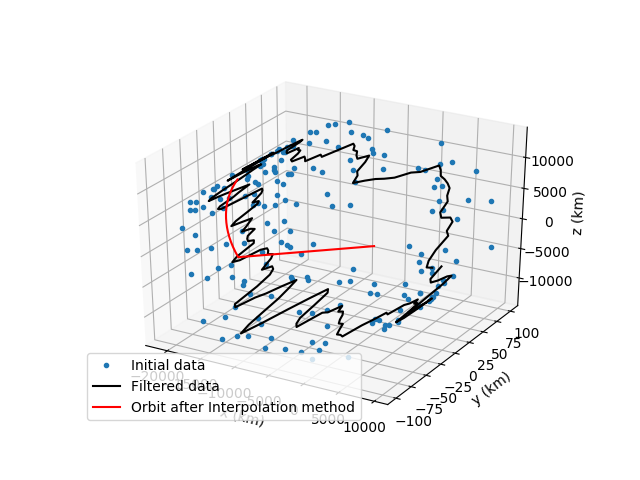
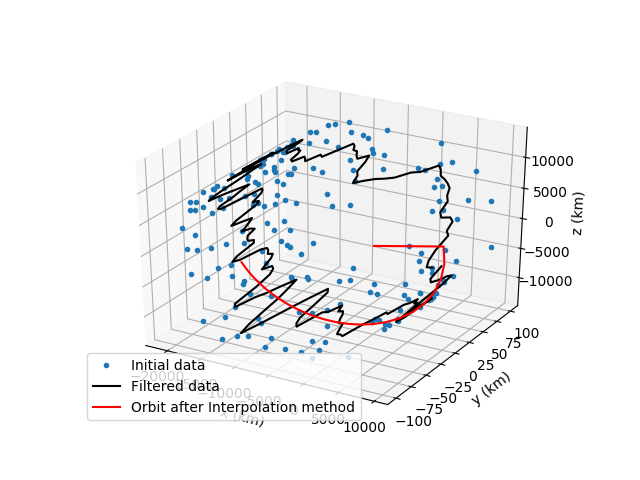
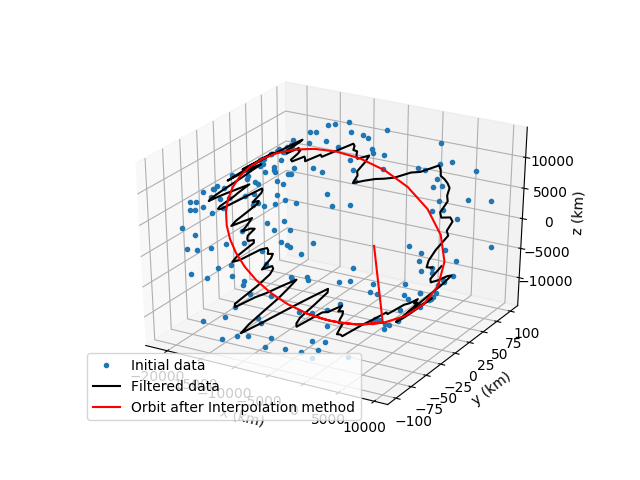
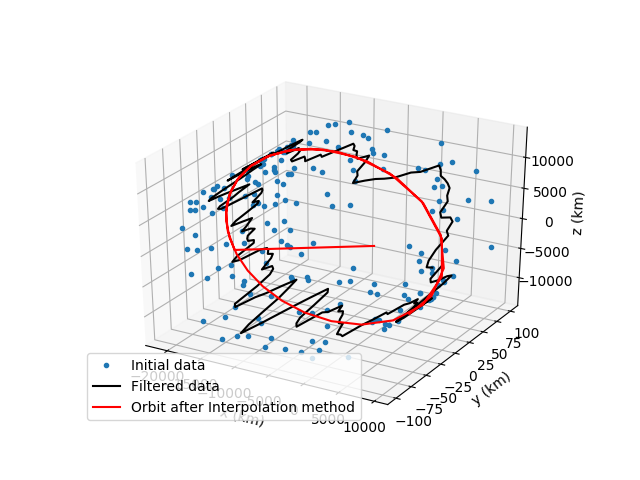
Before moving onto the list of all the scripts I wrote and the future plans we as a team have for the project I would like to showcase some interesting photos that really describe the whole process of the program we built so far. It showcases the initial data, the filtered data after the first smoothing algorithm, after both first and second and then the creation of the final satellite orbit.
List of the scripts I created
- filters/sav_golay.py
- kep_determination/lamberts_kalman.py
- util/golay_window.py
- util/input_transf.py
- util/kep_state/py
- util/rkf78.py
- util/state_kep.py
- tests/check_keplerian.py
- tests/input_transf.py
- tests/kalman.py
- tests/lamberts_kalman.py
- tests/orbit_trajectory.py
- tests/sav_golay.py
- tests/statekep_kepstate.py
- kep_determination/gibbs.py
- orbit_data/new_orbit_test.py
- setup.py
- main.py
Future plans
- More sophisticated 3d graph output
- Test the program with real-time data coming from a ground station of AerospaceResearch.net
- Reduce computational time for Gibbs method
- Add more filters and keplerian-elements determination methods
- After all of the above register the package to Pypi
Difficulties
First of all, I would like to point out the fact that I am not a computer science student and at first I was really anxious if I could meet the expectations of the project. I had to learn lots of new things and many things that other student programmers already knew. For example, my first encounter with Github was at this Google summer of code program. So, I dedicated lots of time to get familiar with the tools I was going to use to create the project. Tools like Github, Travis CI, pytest, Read the docs, packaging etc. All of these were something new for me and I really enjoyed this learning process as programming is one of the two passions I have. The other one is space applications and that was the other reason I really wanted to apply for this particular project, which I think it was the best fit for me. Finally, the testing of the scripts with that large number of different data sets was a big challenge for me and I really put much time and effort to this part.
Acknowledgements
I would really like to thank Andreas Hornig for his great mentoring and aid throughout the whole part of the program. I am really thankful for this experience I had and really hope me and Nilesh can continue the work for future development of the project.I would also like to thank Google for this initiative, which brings a lot of open-source developers together to create new exciting applications. It was a pleasure being part of 2017 Google summer of code and I will definitely suggest it to any fellow student.
Personal Info
Alexandros Kazantzidis
email: alexandroskaza23@gmail.com
facebook: https://www.facebook.com/alexandros.kazantzidis1
github: https://github.com/Alexandros23Kazantzidis
Project and company’s info
Orbit position data analysis and interpolation
github repository: https://github.com/aerospaceresearch/orbitdeterminator
documentation:
http://orbit-determinator.readthedocs.io/en/latest/?badge=latest
company’s page: https://aerospaceresearch.net/