Hello World!
I have been selected to work for AerospaceResearch.net under the Google Summer of Code program. Since I am a new contributer here, I think I should give a short introduction first. I am Arya Das, an undergraduate student of computer science at Indian Institute of Technology, Patna. I am highly passionate about space. I am also interested in robots, flight simulators, playing piano and swimming.
In this blog post I am going to describe my experience so far at AerospaceResearch.net and the project I am working on.
Working at AerospaceResearch.net
AerospaceResearch.net is a very good organizations for both beginners and experts. The projects are simple enough for beginners, but interesting enough for experts. It is a small organization, so everyone knows everyone else. There is regular communication between everybody. And everybody is friendly, caring and understanding. We use WhatsApp for communication. So it’s very easy to reach out and send a text. The workload is also relatively less. I work around 4 hours every day. My mentor is Alexandros Kazantzidis. We exchange messages everyday and conduct a Skype call every week and discuss what to do next. For keeping track of the project we use a Trello board. Overall this is a fun organization to work with. There are some other benefits of working here that other typical organizations don’t have:
- You get an aerospaceresearch.net email address!
- You get to know many people working in space.
- You can write a paper on your work after the GSoC program.
- Your chances of attending space conferences increase.
DGSN and Orbit Determinator
I am working on the Orbit Determinator project. It will eventually be used alongwith the Distributed Ground Station Network (DGSN) to track satellites and predict their orbits. The DGSN will be a collection of small inter-connected ground stations scattered across the globe. These stations will track cubesats and upload their location to a central server periodically. The job of Orbit Determinator is to find the orbital elements of the satellite from this data and predict how the orbit will evolve over time.

At its present stage, a few filtering and orbit determination algoritms have been implemented in Orbit Detrminator. I am working on making this application work with live data. I am also developing a web dashboard for it.
This is how I think the application will work:
- Track the satellite’s position for atleast one full orbit.
- Feed the data into orbit determinator. It gives out a preliminary orbit that closely resembles the actual orbit.
- Use this preliminary orbit to predict where the satellite will be in future.
- Observe the actual location of the satellite.
- Use this observation to correct the prediction. Note that both the prediction and the observation will have errors. So individually, none of them can be trusted. Some filtering algorithm must be used to combine both the results. We are thinking about using the Kalman filter.
- Over time, the model will converge and give accurate predictions for the satellite’s location.
My work over the past two weeks
Over the past two weeks, I developed and tested a new algorithm for preliminary orbit determination. Previously, a variation of Lambert’s method and an interpolation method were being used. Their results were not very good because they were designed with an error of 100km. In reality, the error in observation is around 10km. When I plotted the points, I noticed that they looked like an ellipse. So I deduced that trying to fit an ellipse to the data points would be a good idea. My algorithm, ellipse_fit, has the following steps:
- Fit a plane to the data points. Since the angular momentum of an orbiting body is conserved, all ideal orbits lie on a fixed plane. I observed this when I plotted the data. They all neatly lined up. Fitting a plane gives us the inclination (i) and right ascension of ascending node (Ω).
- Since the observed data has some error, most of the points will not lie on the plane. So as an approximation, we must consider the point on the plane that is closest to the actual point. We can find it by projecting all the points onto the plane.
- Since the plane is a 2D surface, we only need two corrdinates to span it. I chose two orthogonal, unit vectors on the plane as the coordinate axes. Then we find out the coordinates of all the points with respect to these axes.
- Now the problem is a 2D problem. We try to fit an ellipse to the data points. Doing this gives us the semi-major axis (a), the eccentricity (e) and the argument of periapsis (ω).
- Now to find the true anomaly (θ) of any point we find out the angle between it and the periapsis, along the direction of motion of the satellite.
- Thus, all the 6 Keplerian elements have been obtained.
To fit the plane, I first found the average of the cross products between two consecutive positions. This gives the approximate normal vector of the plane. Then I pass it through Nelder-Mead numerical minimization algorithm to refine it even further. This algorithm is included in SciPy. Although it’s not the fastest, it works well with our data.
Fitting the ellipse is more complicated than fitting the plane. Since all orbits have one foci at the center of the parent body, the origin will always be a focus of the ellipse. In such a condition, the equation of an ellipse in polar coordinates is:
We can enter this formula and an initial guess into the Nelder-Mead algorithm and it will give out the optimal values for these parameters. As an initial guess I used these:
where is the maximum radius,
is the minimum radius and
is the angle of the minimum radius.
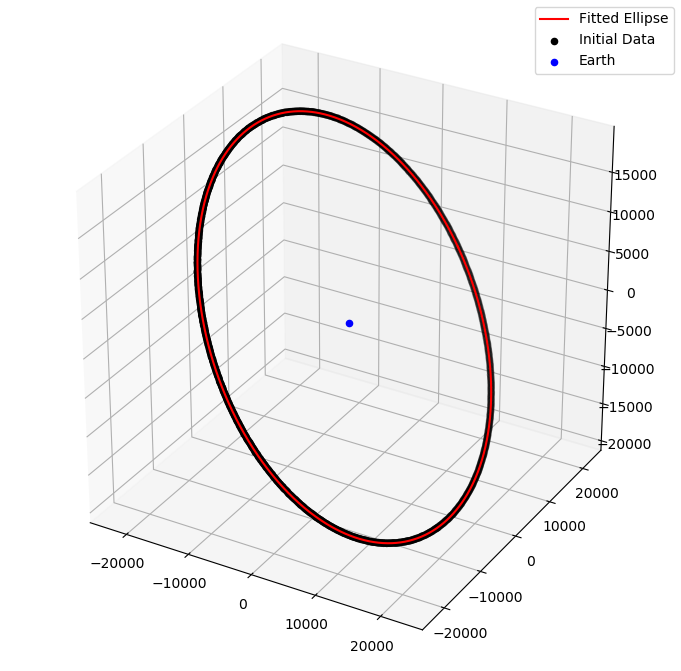
After writing the algorithm I tested it with various satellites. I headed over to https://www.celestrak.com/NORAD/elements/ and downloaded the TLE of various satellites. Then I converted the TLE into a state vector. I generated more state vectors using Runge-Kutta 5 numerical integration algorithm which was developed last year. I added some noise to this data, fed it to ellipse_fit and compared the results. It gives pretty accurate results, which can be found here. I tested ellipse_fit with the following satellites:
- NOAA-1
- NOAA-15
- NOAA-18
- NOAA-19
- Cryosat-2
- GPS-23
- Molniya-2-10
- ISS
These satellites have been added as unit tests. I did some other miscellaneous things these couple of weeks:
- Wrote the script to convert TLE into state vector.
- Added Google style documentation to all the scripts I created.
- Learnt about Dash and made a basic template for the web app.
That’s it! That was my first couple of weeks of GSoC. It was a good learning experience. I am looking forward to making more impressive things this summer.