Angles-only orbit determination: implementation of Gauss method
During these weeks, I worked towards implementing Gauss method for preliminary orbit determination using only angle measurements of a celestial body, either for Sun-centered (heliocentric, e.g., asteroids, comets, planets) or Earth-centered (geocentric, e.g. artificial satellites, space debris) orbits. Gauss method is able to take, for a given celestial object, only three pairs of right-ascension and declination observations, as seen from the surface of Earth, and compute an orbit from only those three observations.
In order to implement Gauss method, I followed closely the text from Howard D. Curtis, „Orbital Mechanics for Engineering Students“, specially section 5.10. For more details about the math behind the method, the reader is referred to this book.
The core idea and implementation
Gauss method may be summarized as follows: if we know the geodetic latitude phi_deg, the altitude above the reference ellipsoid altitude_km, the flattening of the Earth f; and if we have a list of three right ascensions ra_hrs and three declinations dec_deg associated to an observed celestial object, as well as the local sidereal time associated to those three observations lst_deg, and the time elapsed between them t_sec, then we are able to compute the cartesian state of the celestial body, referred either to the Sun or to the Earth, depending on the nature of its orbit. Here, we note that each one of ra_hrs, dec_deg, lst_deg and t_sec are lists with exactly three elements. Also, we note that the right-ascension and the declination determine the line-of-sight (LOS) of the celestial object with respect to the observer. Thus, we are able to write a function like this:
def gauss_method(phi_deg, altitude_km, f, ra_hrs, dec_deg, lst_deg, t_sec)
and the output of this function is the cartesian position r2 = [x,y,z] and the cartesian velocity v2 = [u,v,w] of the object, at exactly the time of the second observation.
A crucial detail
The output of Gauss method depends crucially on finding the real, positive roots of an 8-th order univariate polynomial, which is solved by means of Newton’s method in the book; we tested this using scipy.optimize.newton, but we actually obtained better numerical stability using numpy.roots, which allows to obtain the roots of an univariate polynomial of arbitrary finite order. One drawback of this method is that, in case of obtaining more than one real, positive roots to the polynomial, then one has to choose manually the root which corresponds to the physical motion of the object. But once the adequate root has been chosen, then the Gauss method gives a very good first estimate of the orbit.
Iterative refinement of Gauss method
Also, the output from the Gauss method may be refined; this involves computing iteratively better and better estimates of the Lagrange functions associated to the cartesian states at the first and third observations, in terms of the cartesian state at the second observation. Again, following the text from the book, we were able to implement the iterative refinement procedure for Gauss method.
Results
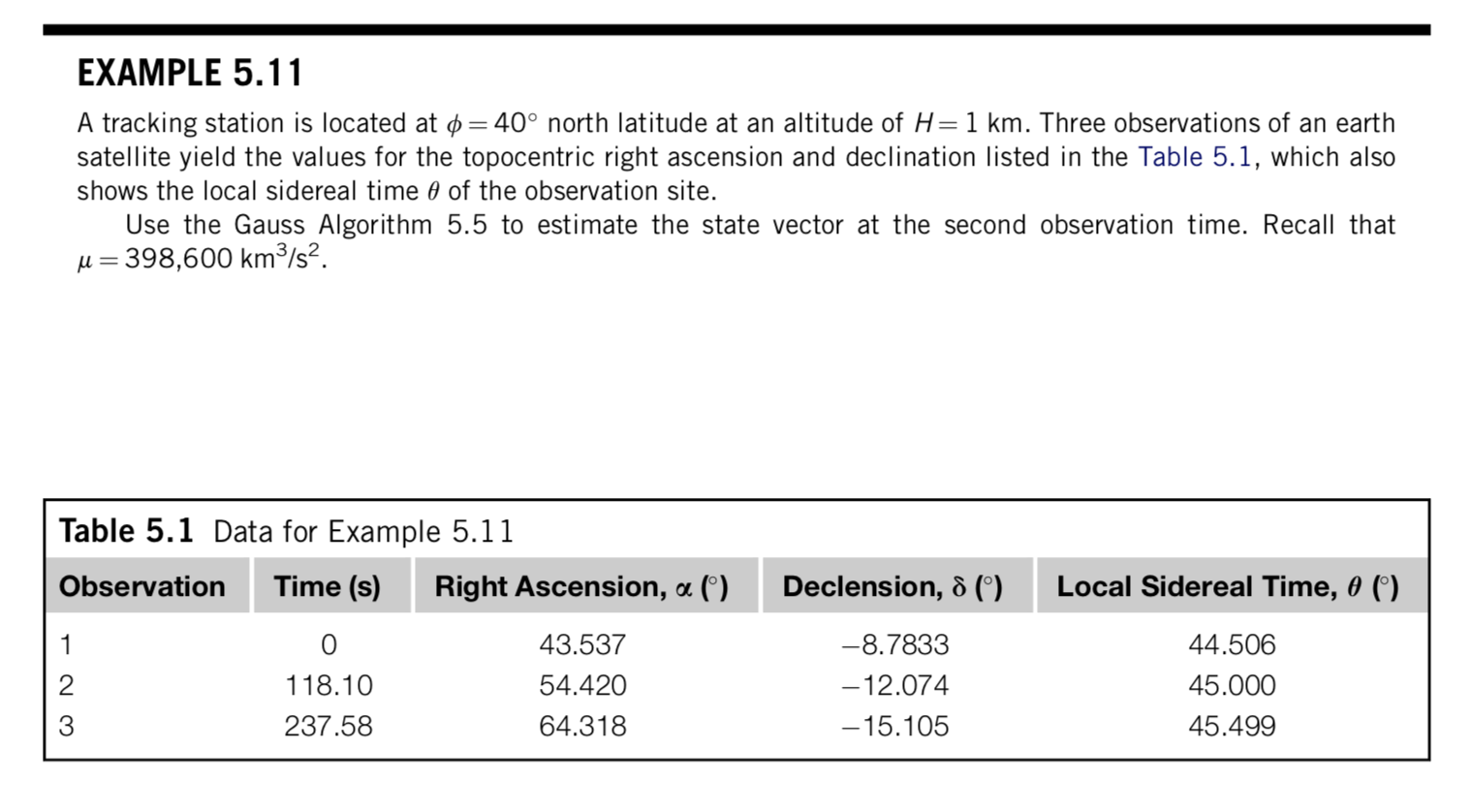
In order to test our code, we followed step-by-step the Examples 5.11 and 5.12 from the „Orbital Mechanics…“ book by H.D. Curtis.
Our results closely follow the numbers cited by the author, although with some small differences, which we attribute to roundoff errors:
Regarding the refinement procedure (Algorithm 5.6), our results show convergence to practically the same values as the ones cited in the book:
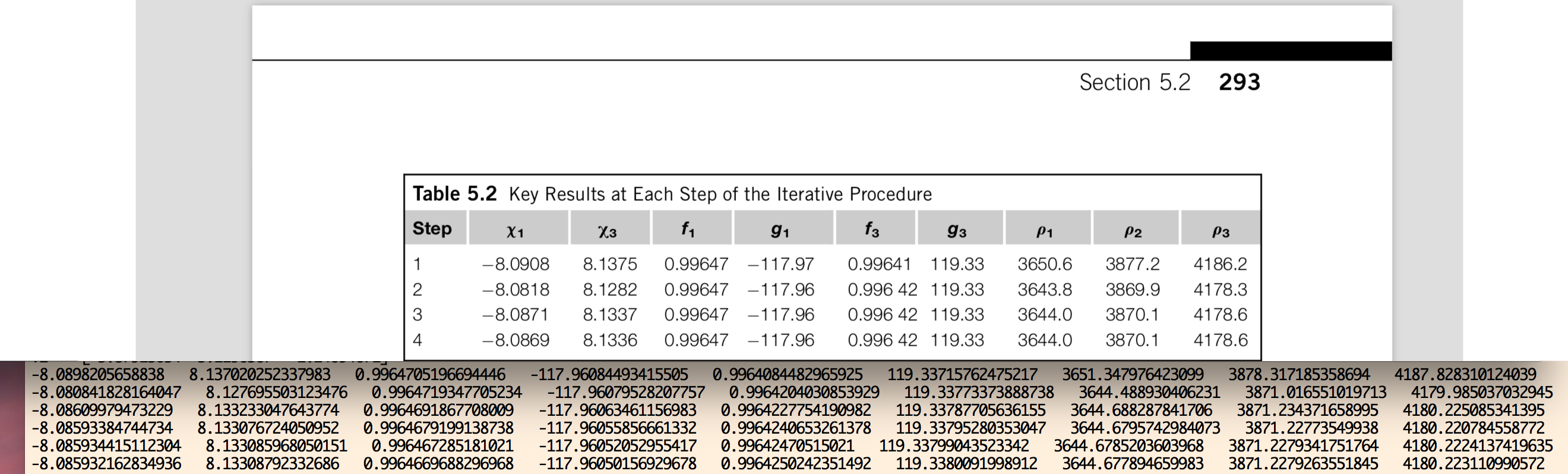
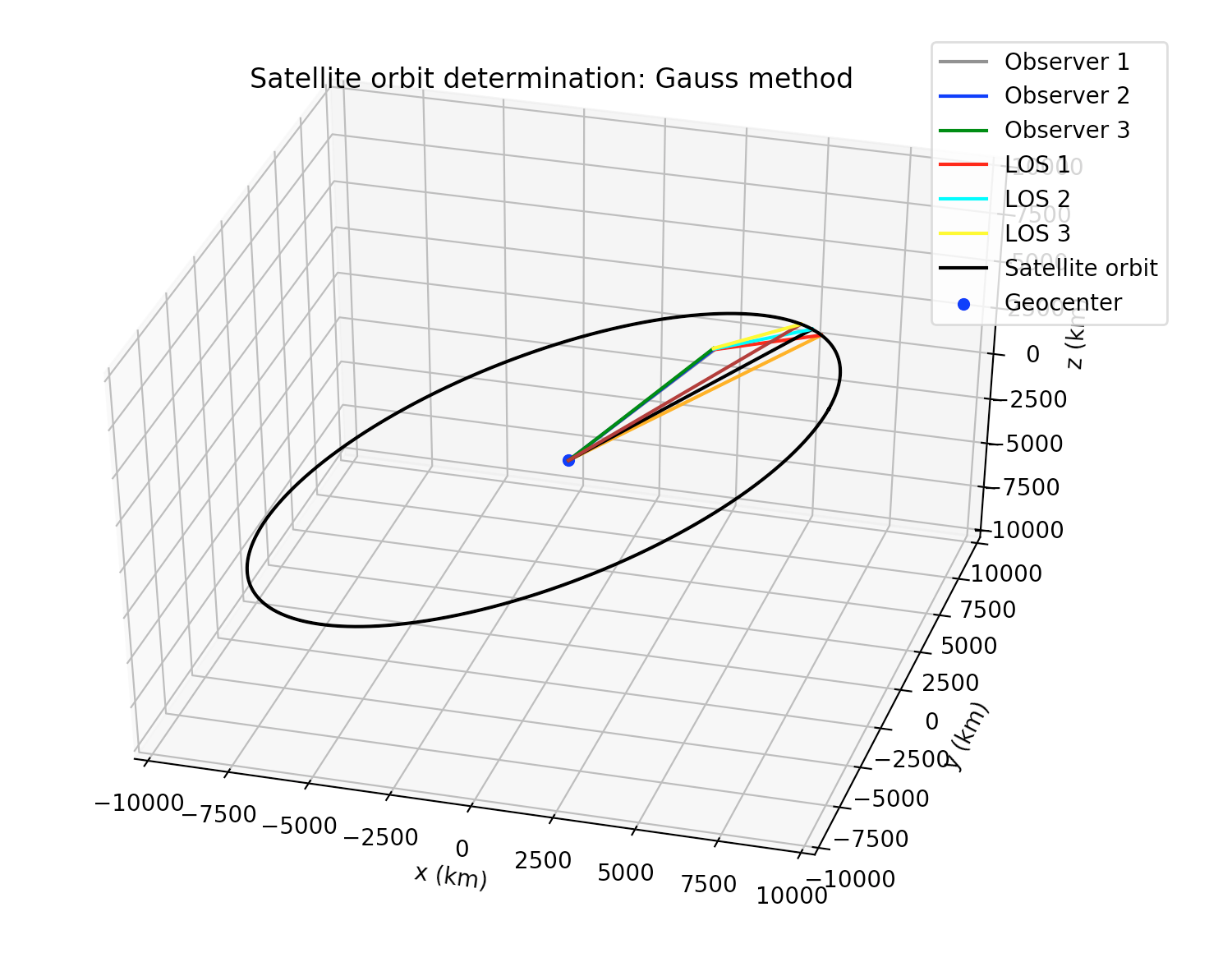
In the figure above, we show a comparison of the numbers we get for each of the quoted variables in the book, for each stage of the refinement iterative procedure for Gauss method. Although some small differences appear, eventually after about 15 to 20 iterations, our code shows convergence up to the precision of 64-bit floating point arithmetic. In the figure below, we show (black) the elliptic orbit corresponding to the output of Gauss method, for the observational data given in Example 5.11 from the book. The „Observer 1“, etc., lines correspond to the geocentric position of the observer on the surface of the Earth; „LOS 1“, etc., correspond to the line-of-sight vectors from the observer to the satellite defined by the RA-dec observations. The orange, black and brown lines correspond to the geocentric cartesian states of the satellite at the time of each observation, computed by means of the Gauss method.
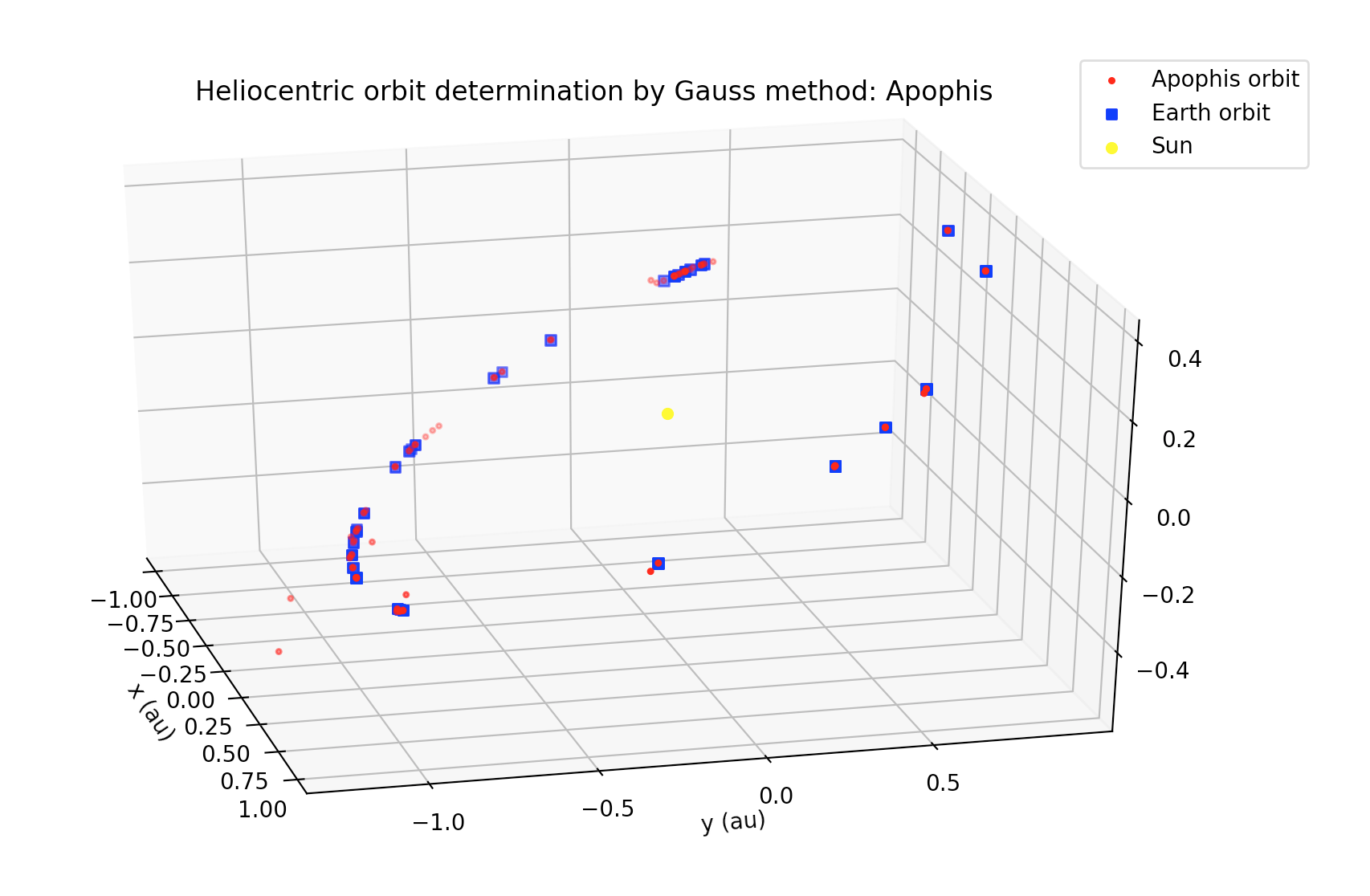
As a second test for our implementation of Gauss method, we took the observational data from the Minor Planet Center (MPC) for asteroid 99942 Apophis, which is a Near-Earth asteroid (NEA). Some differences with respect to Earth-centered orbits are: instead of km for length units and seconds for time units, it is better to use au (astronomical units) and SI days as length and time units, respectively. Besides, instead of the mass parameter μ=G*m for the Earth, we must use the Sun’s mass parameter (in au³ day¯² units). But one of the main differences of Sun-centered orbits with respect to the Earth-centered orbits, is that in order to compute the position of an observer on the surface of the Earth with respect to the center of the Sun, we must know in advance the position of the center of the Earth with respecto the center of the Sun. In order to achieve this, the Python package jplephem was used, which allow us to retrieve the cartesian state of the center of the Earth wrt to the center of the Sun using the NASA-JPL DE430 planetary and ephemerides.
In the figure below, we show a processing of around 1,000 observations of Apophis, from various observatories from around the world, and using our implementation, we were able to reconstruct the orbit of the asteroid around the Sun:
Since the orbit of this asteroid suffers perturbations from the planets, as well as non-gravitational perturbations (e.g., Yarkovsky effect), then a direct application of Gauss method gives only a preliminary estimation of its orbit. In order to compute a more accurate orbit, this method has to be combined with other orbit determination methods (e.g., least-squares, etc.).