Autor: Jorge Perez

[GSoC2018|OrbitDeterminator|Jorge] Angles-only orbit determination: Gauss method and least-squares

1. Introduction

During GSoC 2018, I worked on developing a ra/dec angles-only Keplerian orbit determination implementation for AerospaceResearch.net’s orbitdeterminator project. Our implementation incorporates both elements from the Gauss method for orbit determination, as well as from the least-squares principle. I did this both for Earth-orbiting bodies (satellites, space debris, etc.), and Sun-orbiting bodies (asteroids, comets, centaurs, etc.).

My implementation makes use of the astropy library, whose SkyCoord class provided the adequate abstraction in order to perform the required computations. astropy was also really useful for handling of units, angles, longitudes, etc., as well as providing access to the SPK kernel of JPL ephemerides DE432s, which are at the core of the orbit determination for Sun-orbiting bodies. Also, the poliastro library was useful for the evaluation of Stumpff’s functions in order to perform the refinement stages of the Gauss method. Finally, scipy’s functionality allowed the use of the Levenberg-Marquardt method for the least-squares fit to ra/dec observations.

2. Link to my GSoC 2018 project work:

The main part of the work I did is contained in the following modules:

  • orbitdeterminator/kep_determination/gauss_method.py
  • orbitdeterminator/kep_determination/least_squares.py

The pull request associated to my GSoC project is in GitHub at: aerospaceresearch/orbitdeterminator PR #141. My GitHub handle is @PerezHz . You can also find me on Twitter as @Perez_Hz.

3. Gauss method

The orbitdeterminator/kep_determination/gauss_method.py module allows the user to input files which contain ra/dec observations of either Earth-orbiting or Sun-orbiting celestial bodies, following specific formats for each case, and allows to compute an orbit from n>=3 observations.

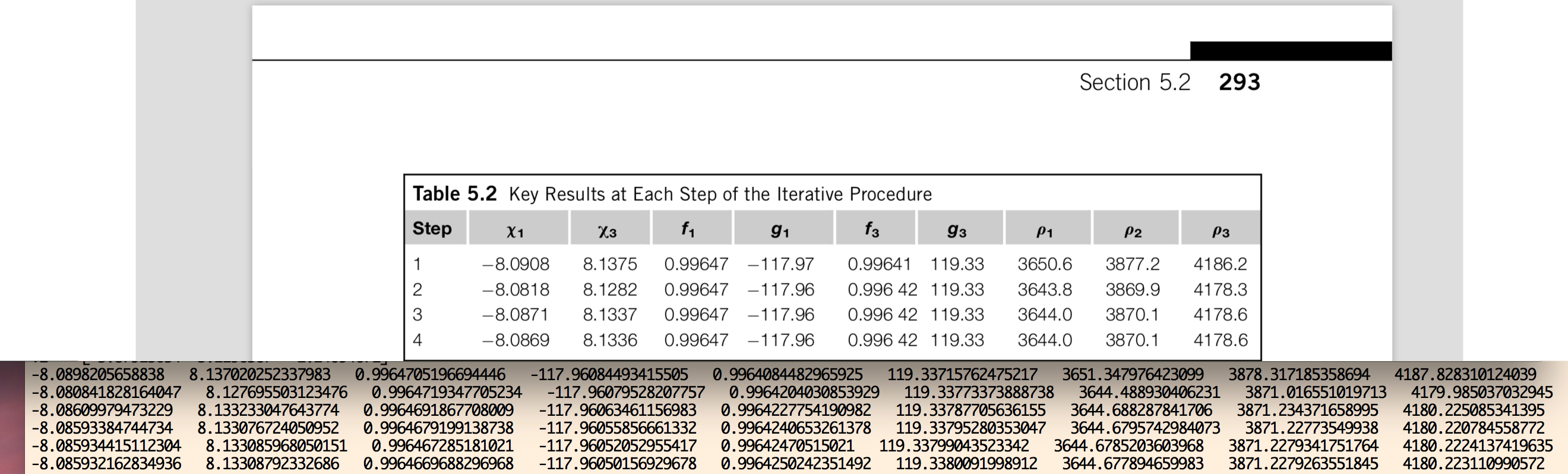
If the number of observations is n==3, then the Gauss method is applied to these 3 observations. Otherwise, if n>3, then the Gauss method is executed over n-2 consecutive observation triplets. A set of orbital elements is computed for each of these triplets, and an average over the resulting n-2 set of elements is returned. A refinement stage has been implemented for the Gauss method such at each iteration of the refinement stage, a better approximation for Lagrange’s f and g functions are computed; which in turn allows to get better estimates for the cartesian state of the observed body.

The right ascension and declination observations topocentric, i.e., they are referred to registered sites either by the MPC or COSPAR. The information about the geocentric position of these sites is contained in registered lists. Both the IOD and MPC formats contain the alphanumeric codes associated to each observation site, so that for each observation it is possible to compute the geocentric position of the observer. This whole process is automatically processed during runtime in the background, so the user does not need to worry about these details.

3.1 Earth-orbiting bodies: gauss_method_sat

The gauss_method_sat function computes Keplerian elements from ra/dec observations of an Earth-orbiting body. The call signature is the following:

gauss_method_mpc(filename, bodyname, obs_arr, r2_root_ind_vec=None, refiters=0, plot=True)

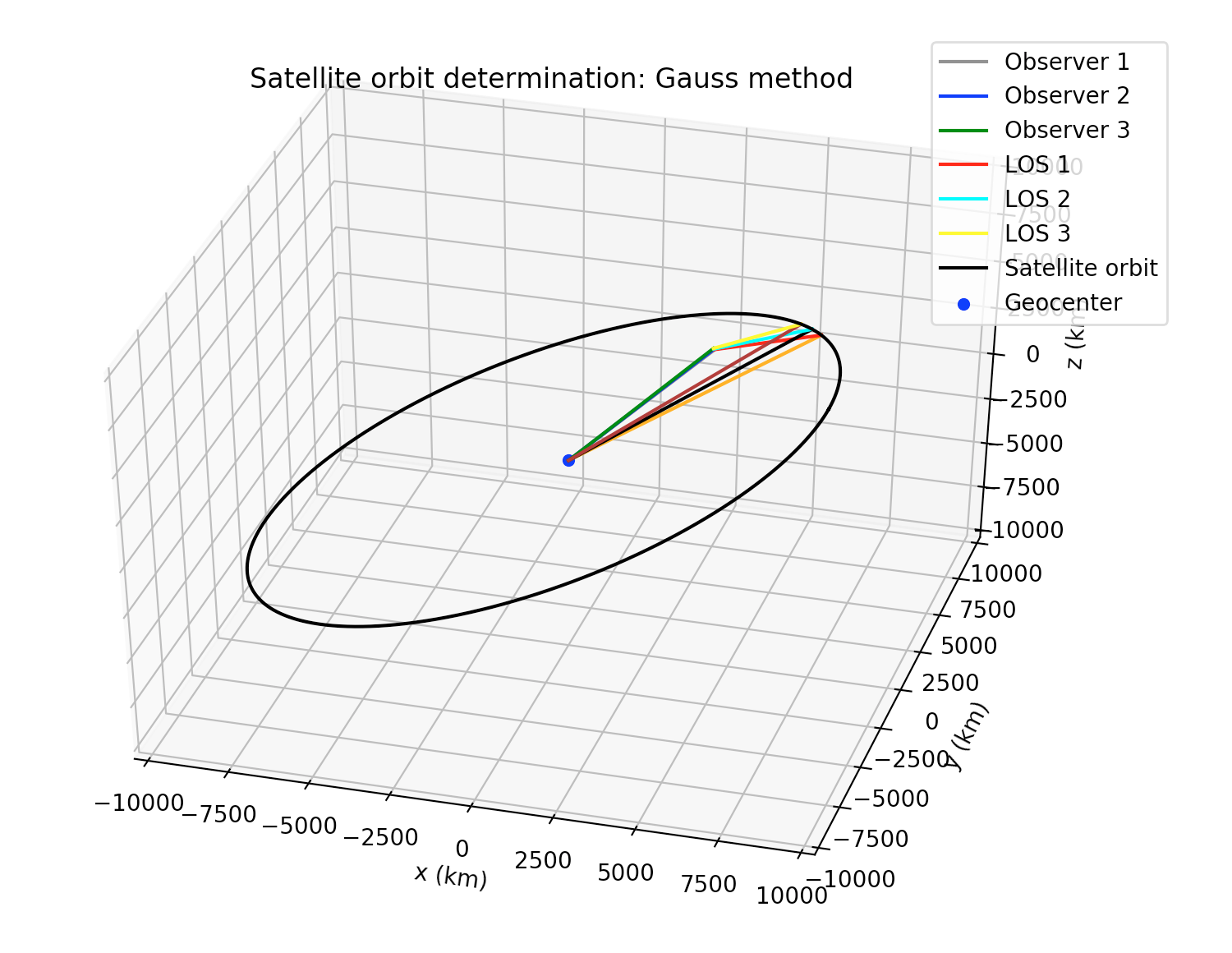
Where filename refers to the name of the file which contains the observations in IOD-format, bodyname is an user-defined name for the observed object, obs_arr is a list/array of integers which define the numbers of the lines in the observation file filename which are going to be processed, r2_root_ind_vec allows the user to select the roots whenever multiple solutions to the Gauss polynomial exist (default behavior is to select always the first root), refiters is the number of iterations for the refinement stage of the Gauss method (default value is 0), and plot is a flag which if set to True will plot the orbit of the object around the Earth. More details may be found at the examples and the documentation. The orbital elements are returned, respectively, in kilometers, UTC seconds and degrees, and they are referred to the (equatorial) ICRF frame. More details may be found at the examples and the documentation.

Example output:

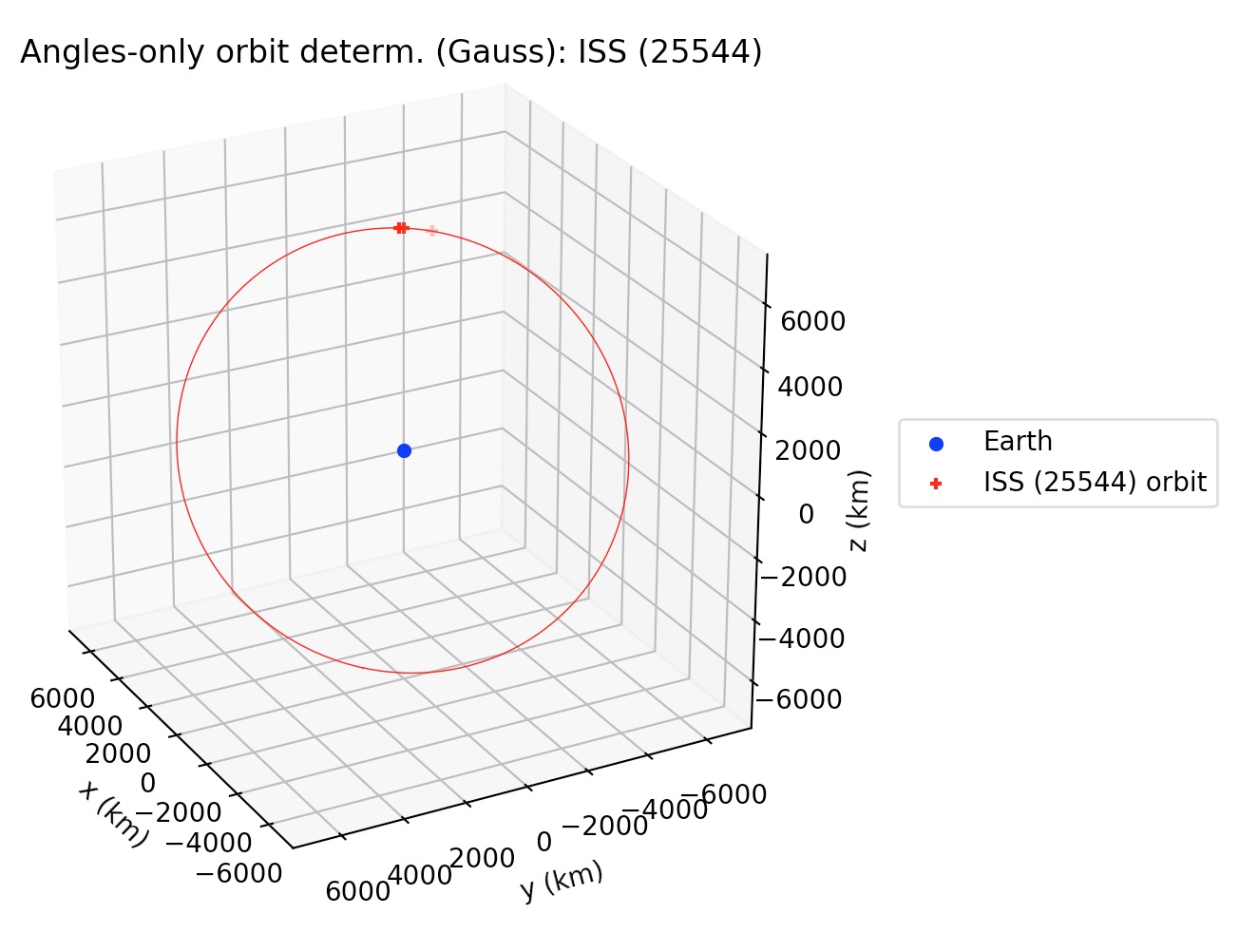
3.2 Sun-orbiting bodies: gauss_method_mpc

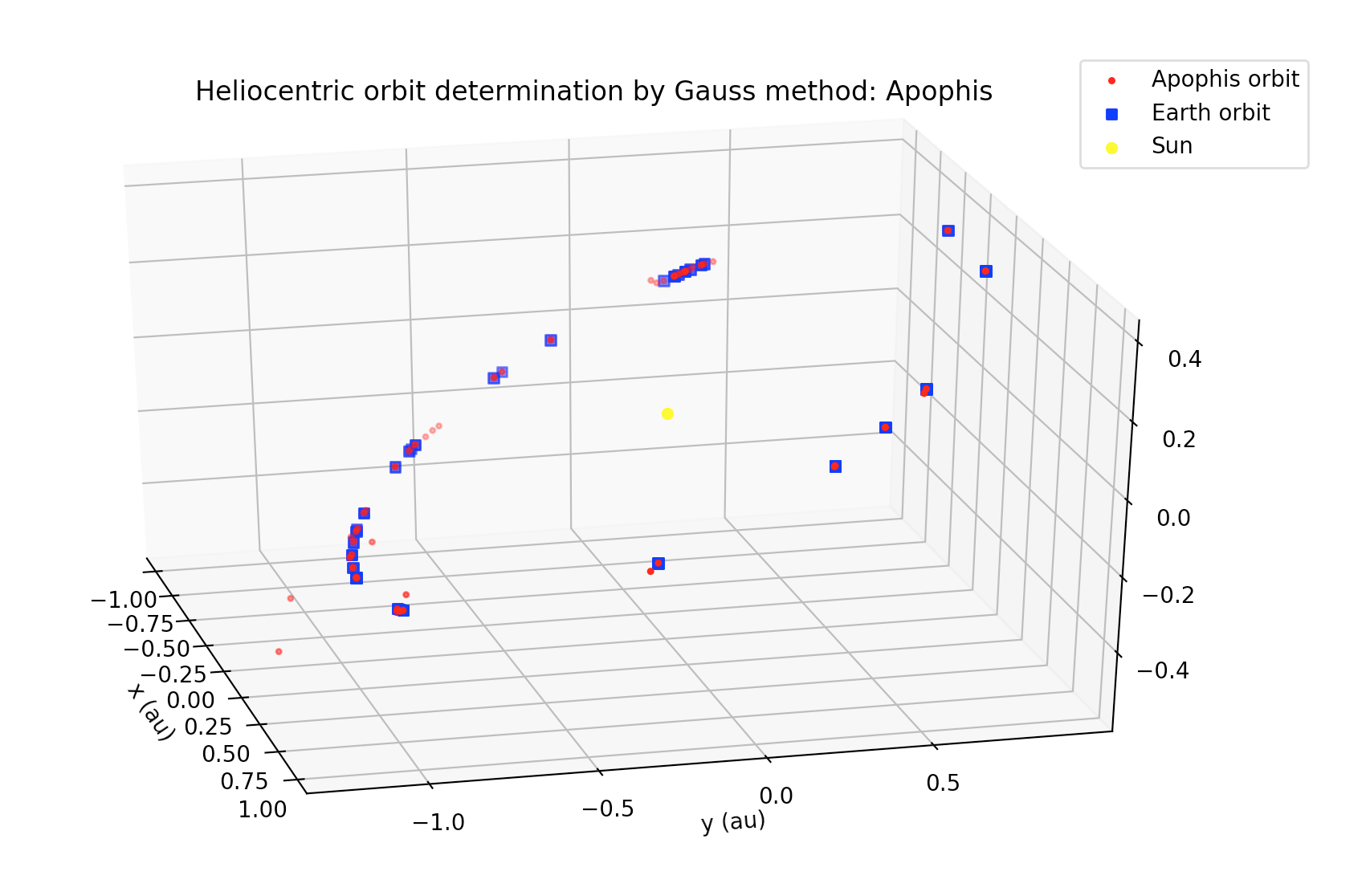
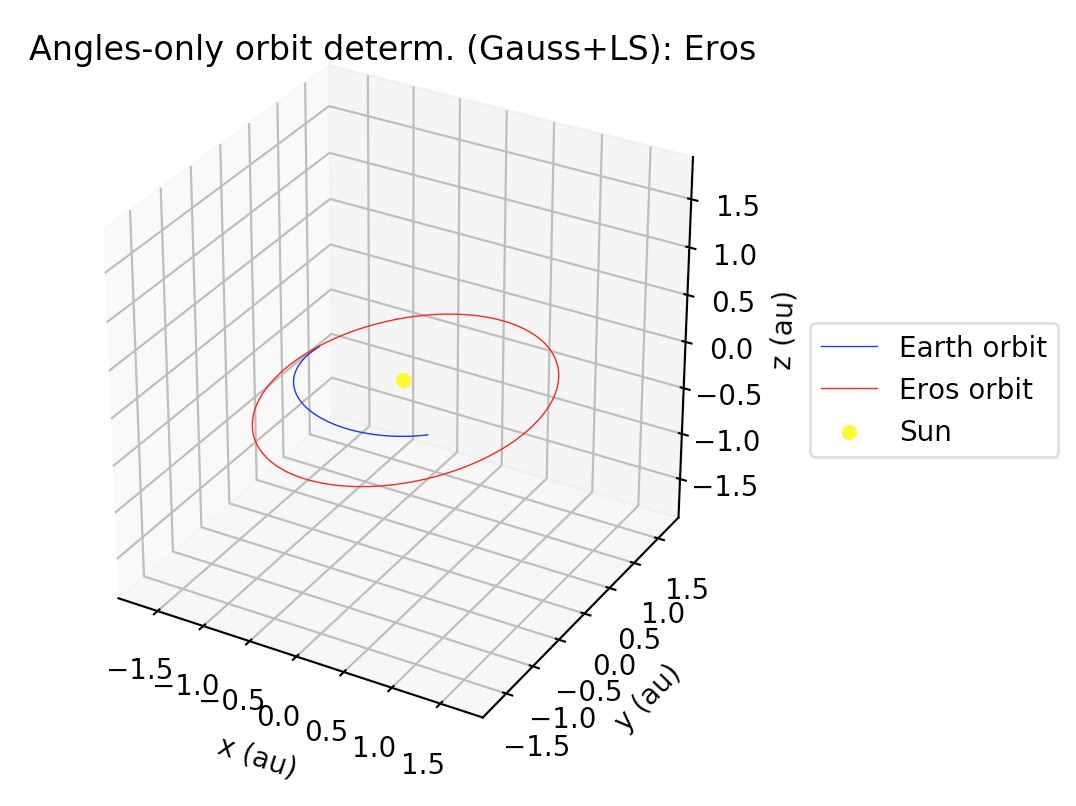
The gauss_method_mpc function computes Keplerian elements from ra/dec observations of an Earth-orbiting body. The call signature is practically same as gauss_method_sat (see section 3.1). One of the differences with respect to the Earth-orbiting case is that in this case the orbital elements are returned, respectively, in astronomical units, TDB days and degrees. But the main difference in the internal processing is that in this case, since the orbit is referred to the Sun, then the position of the Earth with respect to the Sun has to be determined at each of the observation times. gauss_method_mpc uses the JPL DE432s, as provided by the astropy library, in order to compute the heliocentric position of the Earth. This also involves a conversion from the UTC to the TDB time scale, which is also handled again using astropy’s time scale conversion functionalities. Finally, a third difference is that Sun-orbiting orbital elements are returned in the mean J2000.0 ecliptic heliocentric frame. More details may be found at the examples and the documentation.

Example output:

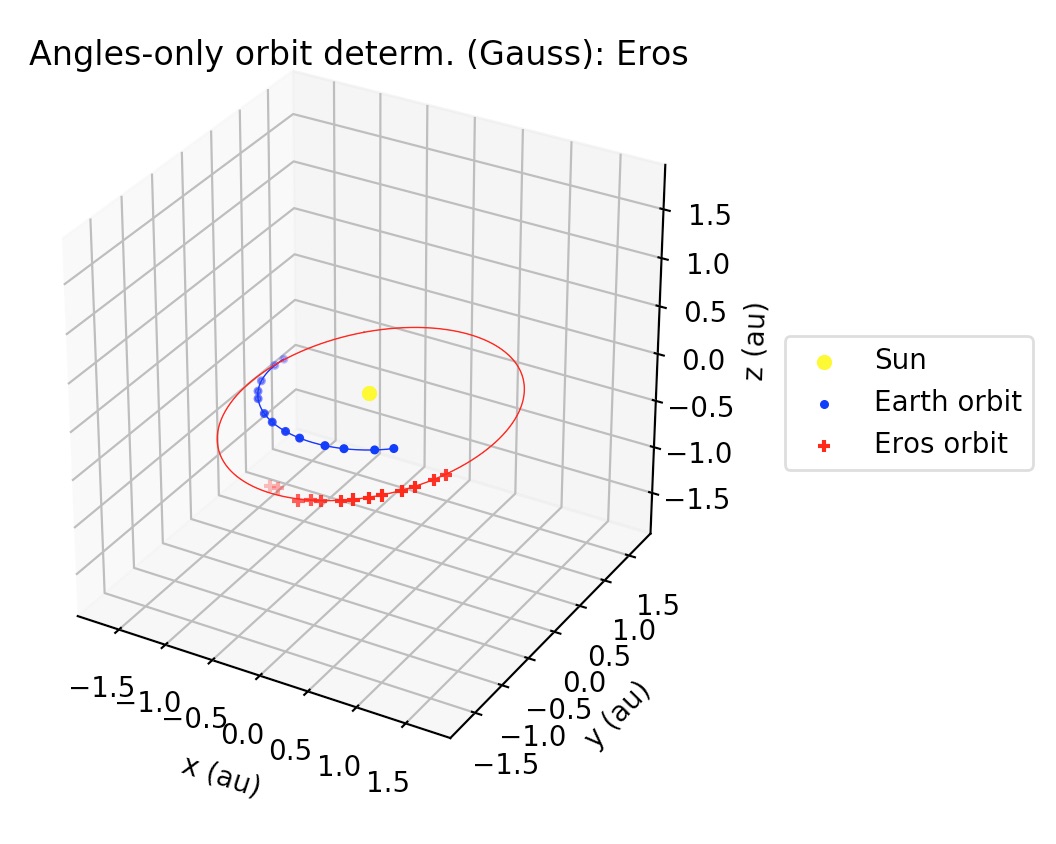
4. Least-squares

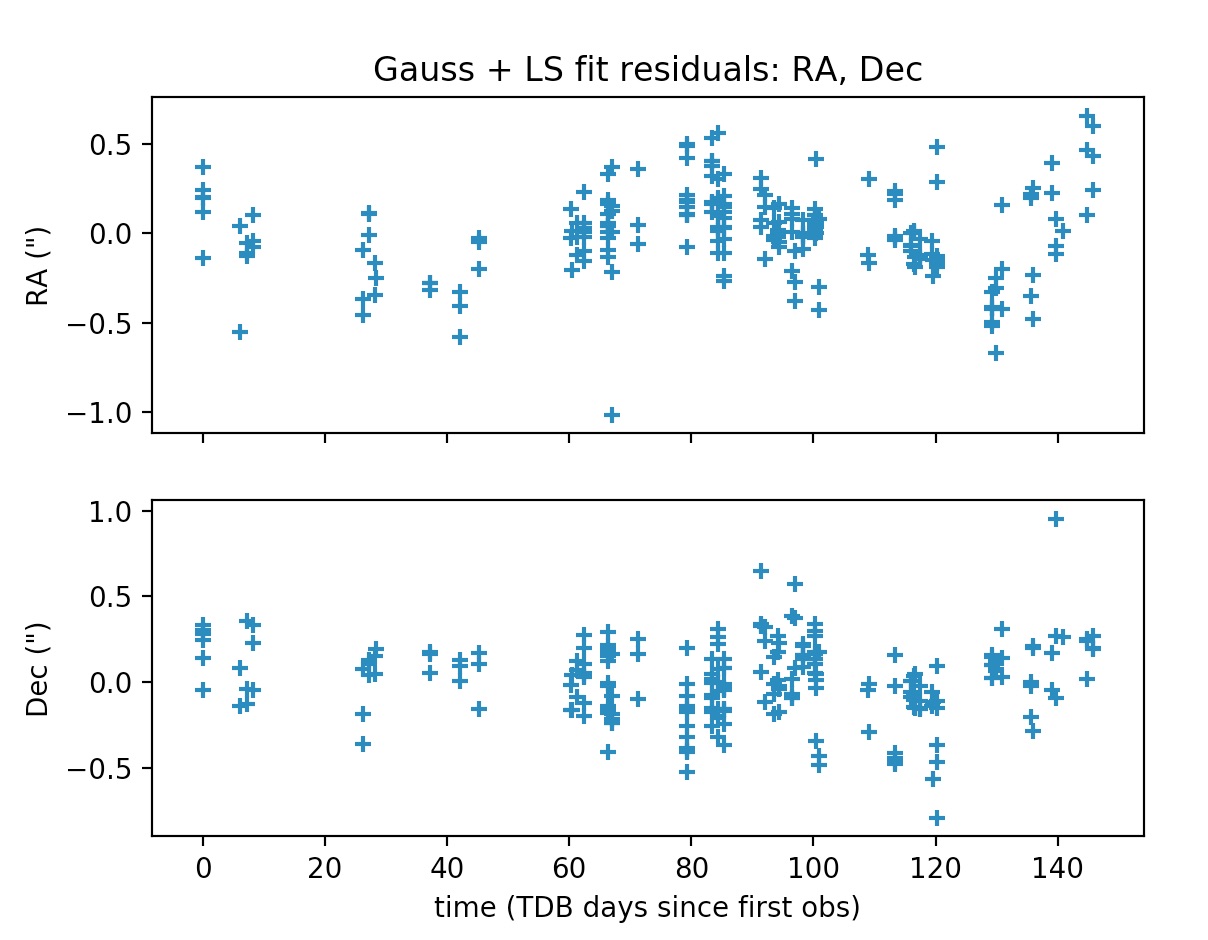
The least-squares functionality developed during my GSoC project may be thought of as differential corrections to the orbits computed by the Gauss method. That is, once a preliminary orbit has been determined by the Gauss method, then the best-fit of the observations to a Keplerian orbit in terms of the observed minus computed residuals (the so-called O-C residuals) may be found by a least-squares procedure. It is worthwhile to mention that in the current implementation all the observations have the same weight in the construction of the O-C residuals vector.

4.1 Earth-orbiting bodies: gauss_LS_sat

Similar to gauss_method_sat in call signature, but after applying the Gauss method to the subset of the observations defined by obs_arr, this function applies a least-squares procedure to the whole set of observations (unless otherwise selected by the user using the optional argument obs_arr_ls; see documentation), returning the Keplerian elements of the best-fit to the observations. Orbital elements are returned in kilometers, UTC seconds and degrees, and they are referred to the (equatorial) ICRF frame. More details may be found in the documentation and the examples.

Example output:

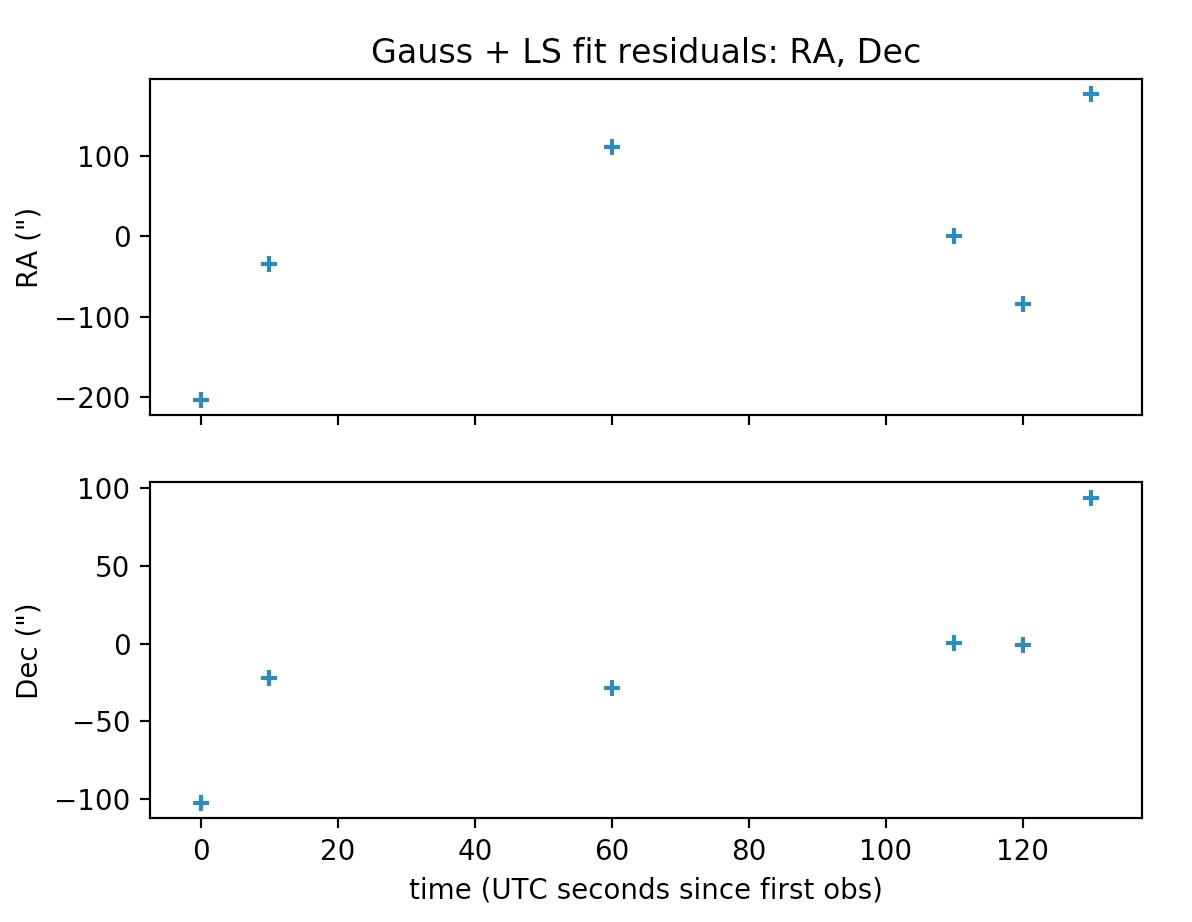
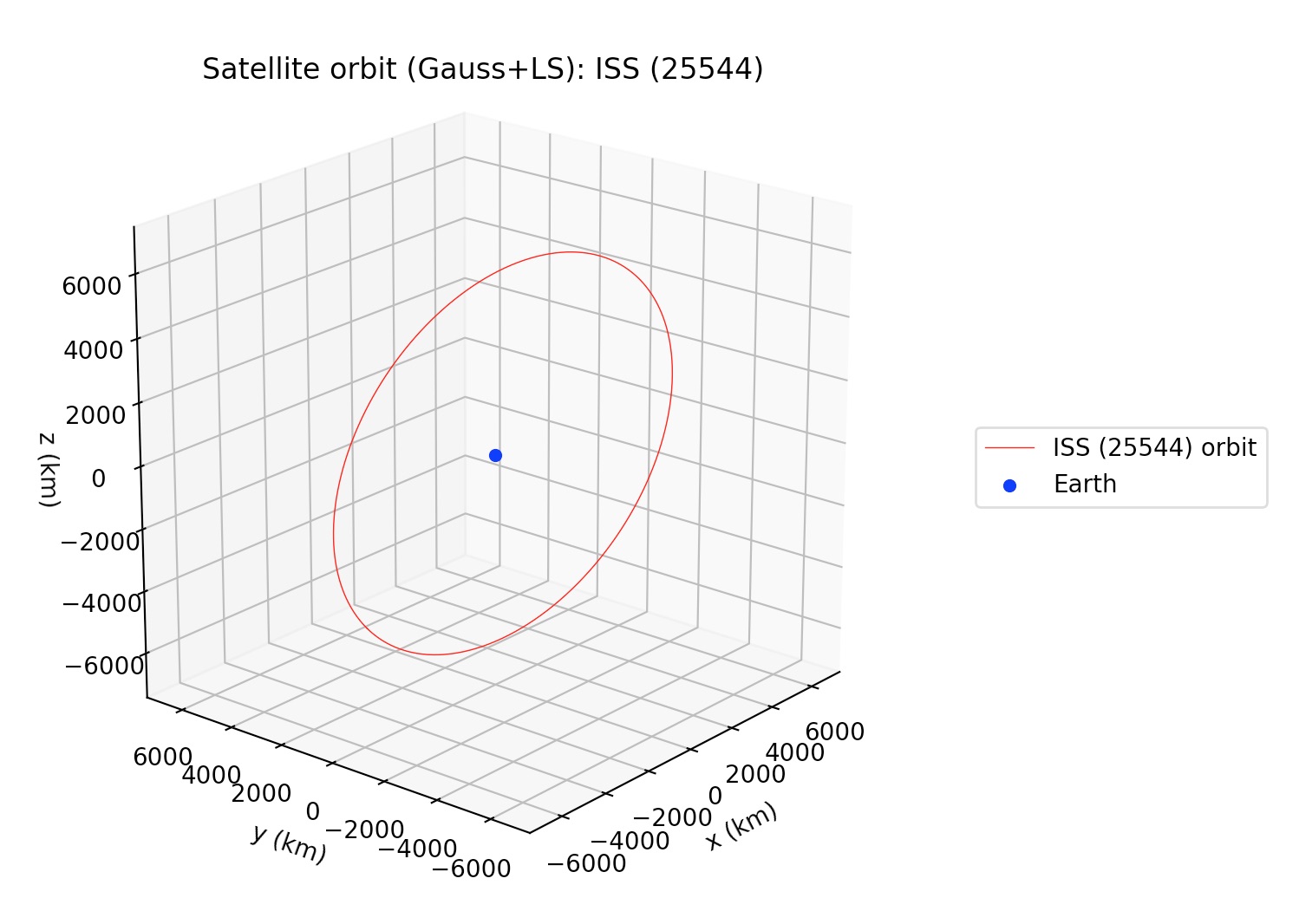
4.2 Sun-orbiting bodies: gauss_LS_mpc

Similar to gauss_method_mpc in call signature, but after applying the Gauss method to the subset of the observations defined by obs_arr, this function applies a least-squares procedure to the whole set of observations (unless otherwise selected by the user using the optional argument obs_arr_ls; see documentation), returning the Keplerian elements of the best-fit to the observations. Orbital elements are returned in astronomical units, TDB days and degrees, and they are referred to the mean J2000.0 ecliptic heliocentric frame. More details may be found at the examples and the documentation.

Example output:

5. Acknowledgments and credits

We wish to thank the satobs.org community, who gave us valuable comments and suggestions, and also provided us with observations of the ISS and other civilian satellites. We also wish to thank the Mathematical Physics group at the University of Pisa, for all the helpful discussions and feedback which contributed to this work.

6. TODOs

  • Allow the user to select ephemerides from astropy: currently, the user is not allowed to specify the ephemerides to be used in the orbit determination of Sun-orbiting bodies.
  • Add perturbations: for Sun-orbiting bodies, add planetary and non-gravitational perturbations; for Earth-orbiting bodies, add oblateness and atmospheric drag to orbit model.
  • For IOD-formatted files, allow the use of other „angle subformats“. There are actually 7 ways to codify the angles in IOD format, but currently the code only allows the angle subformat 2. Subformat 2 was chosen because it is the most used in the Satobs community. Some of this subformats involve alt/az measurements, so in a future version the code should know how to handle alt/az measurements in addition to ra/dec measurements. This could be done, e.g., by using the (alt, az) -> (ra, dec) conversion functions from the astropy library.
  • Implement orbit determination algorithms for SDP/SGP4 models from ra/dec measurements.
  • Let the user choose between two possible values for the signed difference between two angles, instead of always choosing the shortest signed difference by default.
  • Add support for new or non-listed observatories in the MPC or the COSPAR lists of registered observatories.
  • Take into account the finite light propagation time, as well as atmospheric refraction.
  • Add support for radar delay/Doppler observations of Sun-orbiting bodies.
  • Add support for non-equal weights in least-squares subroutines.

 

[GSoC2018|OrbitDeterminator|Jorge] Week #7-8 – Refining Gauss method implementation

During these weeks, I worked on coding a high-level interface for two Gauss method applications of orbit determination: Earth satellites and asteroids.
One of the main differences with respect to my previous work, is that we relied heavily on the astropy library (www.astropy.org), a Python library for astronomical calculations. One of the main factors which inclined us to use this library, is that it has a lot of useful functions, it is relatively well-tested, gives more consistency to the code, and also avoids typos (e.g., in numerical values of astronomical constants). We also incorporated the poliastro library, mainly to use its implementation of the Stumpff functions.

Changes in implementation

One of the main changes with respect to the previous version of our implementation, was the abstraction of a „core“ computation of the Gauss method and its refinement iterative stage, regardless of the case being handled, whether it is an Earth-orbiting object (satellite, space debris, etc.) or a Sun-orbiting object (main-belt asteroid, Near-Earth asteroid, comet, etc.). This abstraction is implemented in the gauss_method_core and gauss_refinement function, which are low level functions and may be adapted for user-defined applications.
A new feature of the latest version of the code, is that in case of having multiple solutions to the Gauss polynomial, now the user is able to select distinct roots for each occurrence of the multiple solutions. As we will see in examples below, multiple positive solutions to the Gauss polynomial are common when handling real-world data. In the case of finding more than one feasible solution to the Gauss polynomial, the code spits out all the feasible roots found; this allow the user to select the adequate root to the polynomial.
Also, the execution speed was improved for the Near-Earth asteroids case: when handling multiple observations, instead of reading the MPC-formatted file each time and retrieving the relevant triplet of observations, now the file is read only once. Since the observation files from MPC are typically a few thousand lines long, this improved the execution speeds about 10x.
Another important change, is that now the local mean sidereal time is computed using astropy ’s sidereal_time method for SkyCoord objects instead of using our own implementation. While doing this, we were able to identify a bug in our implementation of the computation of the local sidereal time!
Finally, in the case of Sun-orbiting bodies, the average orbital elements are computed in the heliocentric J2000.0 ecliptic frame; this allows us to directly compare our results, for example, with the orbital elements listed in the JPL’s Horizons online ephemeris service.

„[GSoC2018|OrbitDeterminator|Jorge] Week #7-8 – Refining Gauss method implementation“ weiterlesen

[GSoC2018|OrbitDeterminator|Jorge] Week #5-6 – Implementation of Gauss method for Earth satellites and NEAs

Angles-only orbit determination: implementation of Gauss method

During these weeks, I worked towards implementing Gauss method for preliminary orbit determination using only angle measurements of a celestial body, either for Sun-centered (heliocentric, e.g., asteroids, comets, planets) or Earth-centered (geocentric, e.g. artificial satellites, space debris) orbits. Gauss method is able to take, for a given celestial object, only three pairs of right-ascension and declination observations, as seen from the surface of Earth, and compute an orbit from only those three observations.

In order to implement Gauss method, I followed closely the text from Howard D. Curtis, „Orbital Mechanics for Engineering Students“, specially section 5.10. For more details about the math behind the method, the reader is referred to this book.

The core idea and implementation

Gauss method may be summarized as follows: if we know the geodetic latitude phi_deg, the altitude above the reference ellipsoid altitude_km, the flattening of the Earth f; and if we have a list of three right ascensions ra_hrs and three declinations dec_deg associated to an observed celestial object, as well as the local sidereal time associated to those three observations lst_deg, and the time elapsed between them t_sec, then we are able to compute the cartesian state of the celestial body, referred either to the Sun or to the Earth, depending on the nature of its orbit. Here, we note that each one of ra_hrs, dec_deg, lst_deg and t_sec are lists with exactly three elements. Also, we note that the right-ascension and the declination determine the line-of-sight (LOS) of the celestial object with respect to the observer. Thus, we are able to write a function like this:

def gauss_method(phi_deg, altitude_km, f, ra_hrs, dec_deg, lst_deg, t_sec)
and the output of this function is the cartesian position r2 = [x,y,z] and the cartesian velocity v2 = [u,v,w] of the object, at exactly the time of the second observation.

A crucial detail

The output of Gauss method depends crucially on finding the real, positive roots of an 8-th order univariate polynomial, which is solved by means of Newton’s method in the book; we tested this using scipy.optimize.newton, but we actually obtained better numerical stability using numpy.roots, which allows to obtain the roots of an univariate polynomial of arbitrary finite order. One drawback of this method is that, in case of obtaining more than one real, positive roots to the polynomial, then one has to choose manually the root which corresponds to the physical motion of the object. But once the adequate root has been chosen, then the Gauss method gives a very good first estimate of the orbit.

Iterative refinement of Gauss method

Also, the output from the Gauss method may be refined; this involves computing iteratively better and better estimates of the Lagrange functions associated to the cartesian states at the first and third observations, in terms of the cartesian state at the second observation. Again, following the text from the book, we were able to implement the iterative refinement procedure for Gauss method.

Results

In order to test our code, we followed step-by-step the Examples 5.11 and 5.12 from the „Orbital Mechanics…“ book by H.D. Curtis.
Our results closely follow the numbers cited by the author, although with some small differences, which we attribute to roundoff errors:
Regarding the refinement procedure (Algorithm 5.6), our results show convergence to practically the same values as the ones cited in the book:
In the figure above, we show a comparison of the numbers we get for each of the quoted variables in the book, for each stage of the refinement iterative procedure for Gauss method. Although some small differences appear, eventually after about 15 to 20 iterations, our code shows convergence up to the precision of 64-bit floating point arithmetic. In the figure below, we show (black) the elliptic orbit corresponding to the output of Gauss method, for the observational data given in Example 5.11 from the book. The „Observer 1“, etc., lines correspond to the geocentric position of the observer on the surface of the Earth; „LOS 1“, etc., correspond to the line-of-sight vectors from the observer to the satellite defined by the RA-dec observations. The orange, black and brown lines correspond to the geocentric cartesian states of the satellite at the time of each observation, computed by means of the Gauss method.
As a second test for our implementation of Gauss method, we took the observational data from the Minor Planet Center (MPC) for asteroid 99942 Apophis, which is a Near-Earth asteroid (NEA). Some differences with respect to Earth-centered orbits are: instead of km for length units and seconds for time units, it is better to use au (astronomical units) and SI days as length and time units, respectively. Besides, instead of the mass parameter μ=G*m for the Earth, we must use the Sun’s mass parameter (in au³ day¯² units). But one of the main differences of Sun-centered orbits with respect to the Earth-centered orbits, is that in order to compute the position of an observer on the surface of the Earth with respect to the center of the Sun, we must know in advance the position of the center of the Earth with respecto the center of the Sun. In order to achieve this, the Python package jplephem  was used, which allow us to retrieve the cartesian state of the center of the Earth wrt to the center of the Sun using the NASA-JPL DE430 planetary and ephemerides.
In the figure below, we show a processing of around 1,000 observations of Apophis, from various observatories from around the world, and using our implementation, we were able to reconstruct the orbit of the asteroid around the Sun:
Since the orbit of this asteroid suffers perturbations from the planets, as well as non-gravitational perturbations (e.g., Yarkovsky effect), then a direct application of Gauss method gives only a preliminary estimation of its orbit. In order to compute a more accurate orbit, this method has to be combined with other orbit determination methods (e.g., least-squares, etc.).

[GSoC2018|OrbitDeterminator|Jorge] Week #3-4 – Least squares fit to cartesian positions as a function of time

Introduction

An orbital fit by least-squares is a technique for computing the set of six Keplerian elements which best describe an orbit with respect to a *whole* set of observations.
As the set of Keplerian elements we choose semimajor axis a, eccentricity e, time of perigee passage τ (i.e., how much time has elapsed since the last perigee), as well as the standard Euler angles which describe the orientation of the orbital plane with respecto to the inertial frame: argument of pericenter ω, inclination I and longitude of ascending node Ω. We denote by X the set of these six Keplerian elements; that is, X = (a, e, τ, ω, I, Ω).
A least-squares fit is simply to look the minimum of a scalar (i.e., real-valued) „cost“ function Q(X). The Q function is simply a measure of how well our theoretical predictions, for a given set X of orbital elements, depart from observations. In an ideal world, we could find a set of orbital elements such that it perfectly matched the observations and thus Q(X)=0. Nevertheless, real-world measures carry uncertainties, and we can only hope to find orbital elements X which make Q attain its minimum possible value with respect to all the observations we have made.
The values of the cost function Q(X) for a least-squared problem are constructed the following way: take *all* the values you observed (call them v_i), and substract from each of those the values you were expecting to measure for a given set of orbital elements X (say, V_i(X) ). Call each of these differences the residuals, xi_i(X) = v_i-V_i(X) . Then, square the residuals, and sum all the squared residuals. The value you obtain following this recipe, is the value of Q(X).
In practice, the least-squares method finds a local minimum of the cost function by performing an iterative procedure, which needs a good initial „guess“ solution X0; otherwise the procedure may converge to non-feasible results. Hence, it is necessary that the „good“ initial guess be provided by a preliminary orbit determination method.

„[GSoC2018|OrbitDeterminator|Jorge] Week #3-4 – Least squares fit to cartesian positions as a function of time“ weiterlesen

[GSoC2018|OrbitDeterminator|Jorge] Week #1-2 – Look up to the sky and marvel!

Hi, everyone! My name is Jorge Pérez, I’m a Physics PhD student at UNAM, Mexico, and this year I have been honored to form part of Aerospaceresearch.net as a GSoC student. Since I am a Python newbie, in these lines, I will try to follow the great Kepler, who in the Preface of his New Astronomy wrote:

What matters to me, is not merely to impart to the reader what I have to say, but above all to convey to him the reasons, subterfuges, and lucky hazards which led me to my discoveries. When Christopher Columbus, Magellan and the Portuguese relate how they went astray on their journeys, we not only forgive them, but would regret to miss their narration because without it the whole grand entertainment would be lost.

So, indeed, even when these last few days have been about warming up, I have been learning a lot. As a first task for my GSoC project, I have been coding some Python functions which will allow orbitdeterminator to load data from text files which contain position observations of either satellites or natural bodies, such as Near-Earth Asteroids (NEAs). Observational data for these type of objects is usually written to text files following fixed-width column formats. That is, in this kind of text files, for example, column 1 to 5 might refer to a numeric ID of the observed object; etc…

As a first thought to implement this, since these formats are defined via columns, my idea was that it might be safer to read these files using Python’s native file reading functions. And I was indeed able to read formatted files and save them into a Python list, but then I would have had to convert that to e.g. a numpy array, or something similar, in order to compute interesting stuff from the data.

So, as a second option, and after learning more about numpy, I thought that the `numpy.loadtxt` function might be the best approach, interpreting the whitespaces as delimiters and read each element as a string. This worked for a particular case I was working with, but I wasn’t sure if this approach would work for other formats.

And then, I worked on a third attempt at this. I realized that there was another numpy file-reading function, `numpy.gentfromtxt`. I liked this function better, since it tolerates files with missing values, as well as admitting files formatted with fixed-width columns. So, at the end, this was the approach that I took, and went on to code file-reading functions for some relevant formats which we will be using during the summer.

So now that we have the ability to load actual position data for satellites and asteroids, the next step, besides refining what I already coded, will be to implement orbit determination methods which take into account this kind of observational data from optical instruments, i.e., telescopes. And once this is done, the next step will be to code an orbit determination subroutine for radar observations, which are more subtle to reduce, but we will talk about this in a future blog post.

Incidentally, these last few days in Mexico City have been unusually warm; but tonight this weather, with clear skies and soft winds, allowed one of the most beautiful sights of the rising Moon in Mexico City since I can remember. Let’s not forget to always look up to the sky and marvel!